An Asymmetric Matching Pennies Game
Introducing Mixed Strategy Nash Equilibria
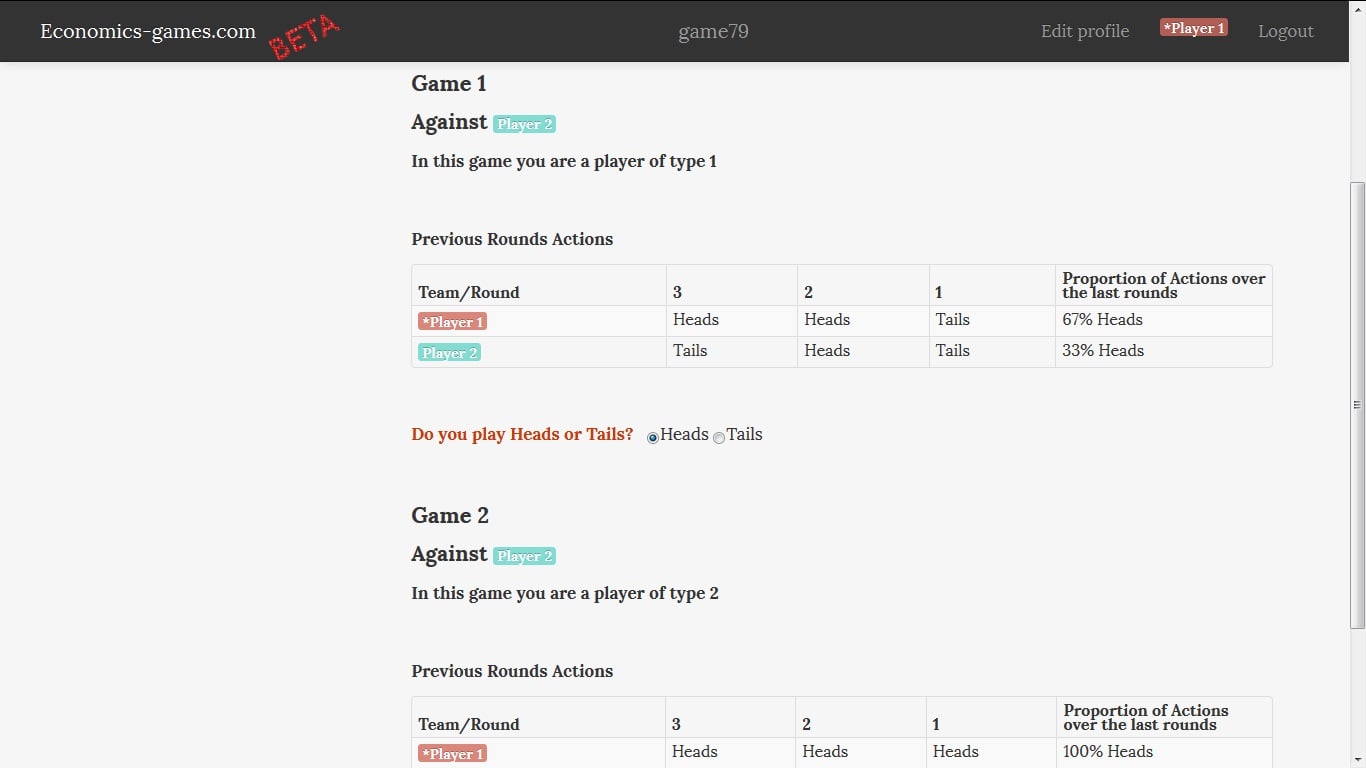
Rules as explained to players:
You will repeatedly play a "coin" game. In this game, you and another player must decide simultaneously either to play "heads" or "tails".
Corresponding payoffs are determined as follows: For one shot of the game, if both players choose the same side, player 2 "gives" (virtually) €5 to player 1. If they choose a different side, player 1 gives €1 or €9 to player 2 (depending on which player plays "heads").
| Player 1 / Player 2 | Heads | Tails |
|---|---|---|
| Heads | 5/-5 | -1/1 |
| Tails | -9/9 | 5/-5 |
In fact, you will play two of these games at the same time, with random players from your class. In one of the two games, you will be a player of type 1, in the other, you will be a player of type 2. You will keep playing with the same two players until the end.
Your overall payoffs are compared to those of everyone else in the class. Your goal is to maximize your payoff, not just to be better than the players you are faced with.
Game details:
This game is particularly interesting to introduce Mixed Strategy Nash Equilibria, and also very intriguing to students.
Behind its seemingly balanced appearance, this is indeed a very biased game: For the mixed strategy nash equilibrium, player 2 gives on average 0.8€ to player 1 for each shot of the game.
Moreover, as is usual for a mixed strategy nash equilibrium, player 1 earns this average 0.8€ whatever the action of player 2 (as long as it chooses heads with a probably of 7/10).
This game has proved to be very effective in capturing students' attention.
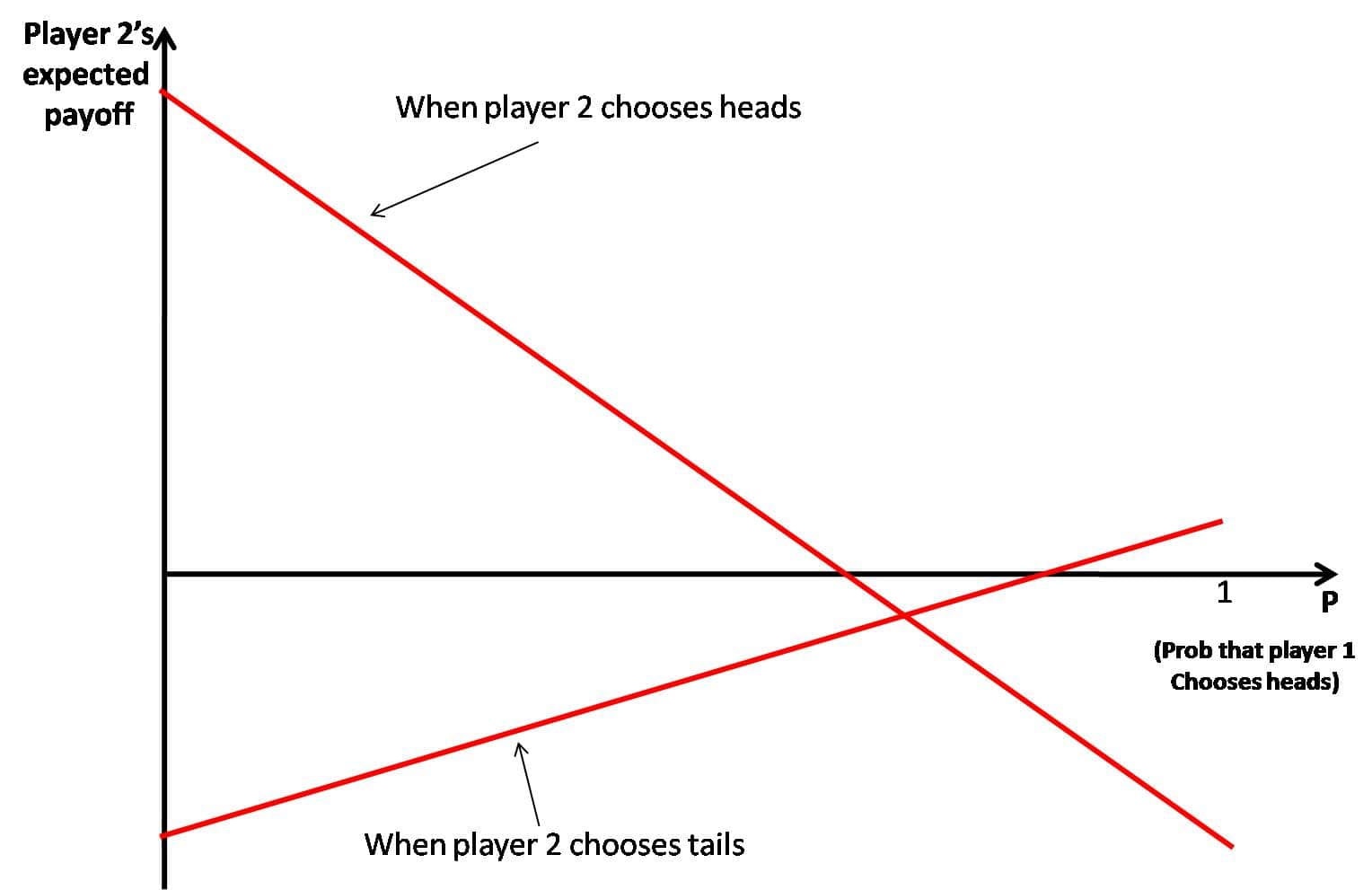
Part of solving the equilibrium. Suppose that player 1 chooses heads with probability p:
- If player 2 chooses heads, its expected payoff is -5p+9(1-p)=9-14p
- If player 2 chooses tails, its expected payoff is 1.p-5(1-p)=6p-5