Industrial Organization Game

Overview of the game

This game involves many important industrial organization concepts. By adapting your debriefings, you can use it either as an introduction to your course, or as an illustration after your lectures. Slides appear regularly to present the rules and draw students' attention to the most important points. All players progress at the same speed.

The game is extremely progressive:

• At the beginning, players only control (dynamic) pricing. This first phase introduces the concept of price elasticity of demand and the principle of price discrimination. But above all, the first year is meant to familiarize players with the interface and the game, and scores are reset to zero at the beginning of year 2.

• During the second year, off-peak periods appear. This is the opportunity to underline the difference between marginal cost and average cost, and emphasize the importance of basing its reasoning on marginal analysis (two questions on the subject appear in the slides of the game).
• From the third year, players also control the number of flights on the route.
• From the fourth year, players can choose the type of aircraft they use.
• From year 5, players can also choose to install more or fewer seats in their planes. The robot-competitors clearly specialize in a low-cost strategy with "few flights with larger aircraft with a lot of seats" and let the players know that. The end of the game allows to introduce the principle of vertical differentiation.

If you run the multiplayer version, you will be able to observe the decisions of the players through your administration interface. It will also provide synthetic information comparing the evolution of prices, airline profits, seats offered and sold, consumer surplus, social surplus, differentiation indexes ...

However, a few trial and error cycles are usually necessary to be able to define a sound strategy, so I would advise you to invite your students to first run the monoplayer variant (located at the top of the games page, first in the monoplayer simulations list): Players will then be able to use the back button to compare different pricing strategies.

Some players may want to go further into technical details. It is possible to carry out computations on game data with these students (unconstrained monopoly prices, optimal dimensioning in the monopoly case, equilibrium prices for the duopoly). I can send you a file with some demand simulations upon request.

In case this can help motivate your students, the highest score (excluding our staff and partners) is currently 194 178 € (and the fifth score, 172 331 €). Above 98 836 € you are in the top 25%, and above 136 471 €, in the top 10%.

The structure of the game

The game has 6 Years. In each "Year", there are only two departure days (from Year 2, one day is in peak period, the other in off-peak period).

Each Year has two Rounds. During the first Round, players only compete to sell tickets for the first departure day (and during the second Round for the second departure day). The departure days are in red on the diagram. The second Round only starts once the first is completed.

There are three Phases during each Round. The first Phase corresponds to the period between three months to one month and a half before departure. The second Phase ranges from one month and a half to two weeks before departure, and the third corresponds to the last two weeks.

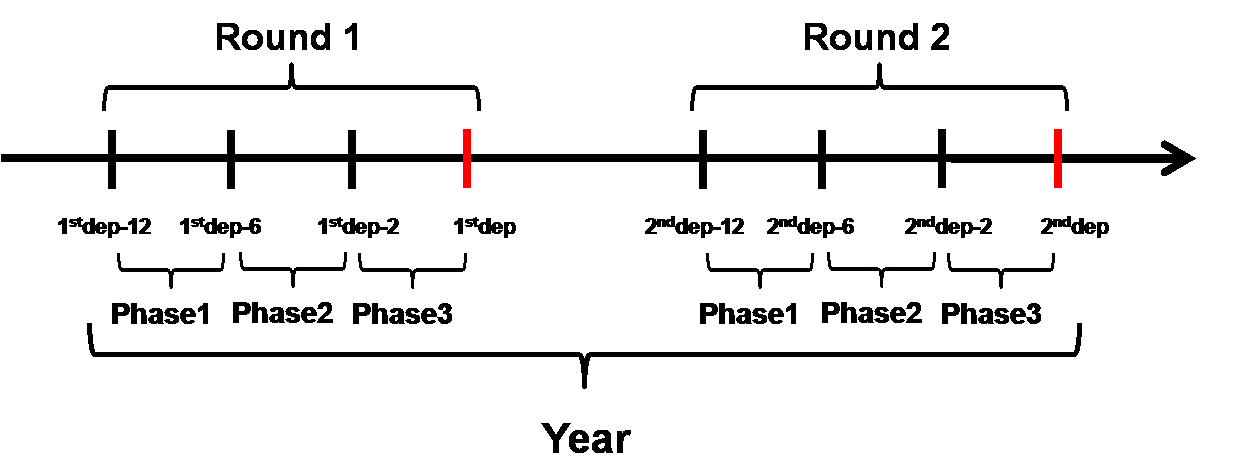
I would suggest you check the demo, the first Year is precisely designed to introduce the game structure.     Demo

Players choose their price for each phase (adapting it to the number of unsold seats). From year 3, they choose the number of flights at the beginning of each year (and from year 4, the type of aircraft).

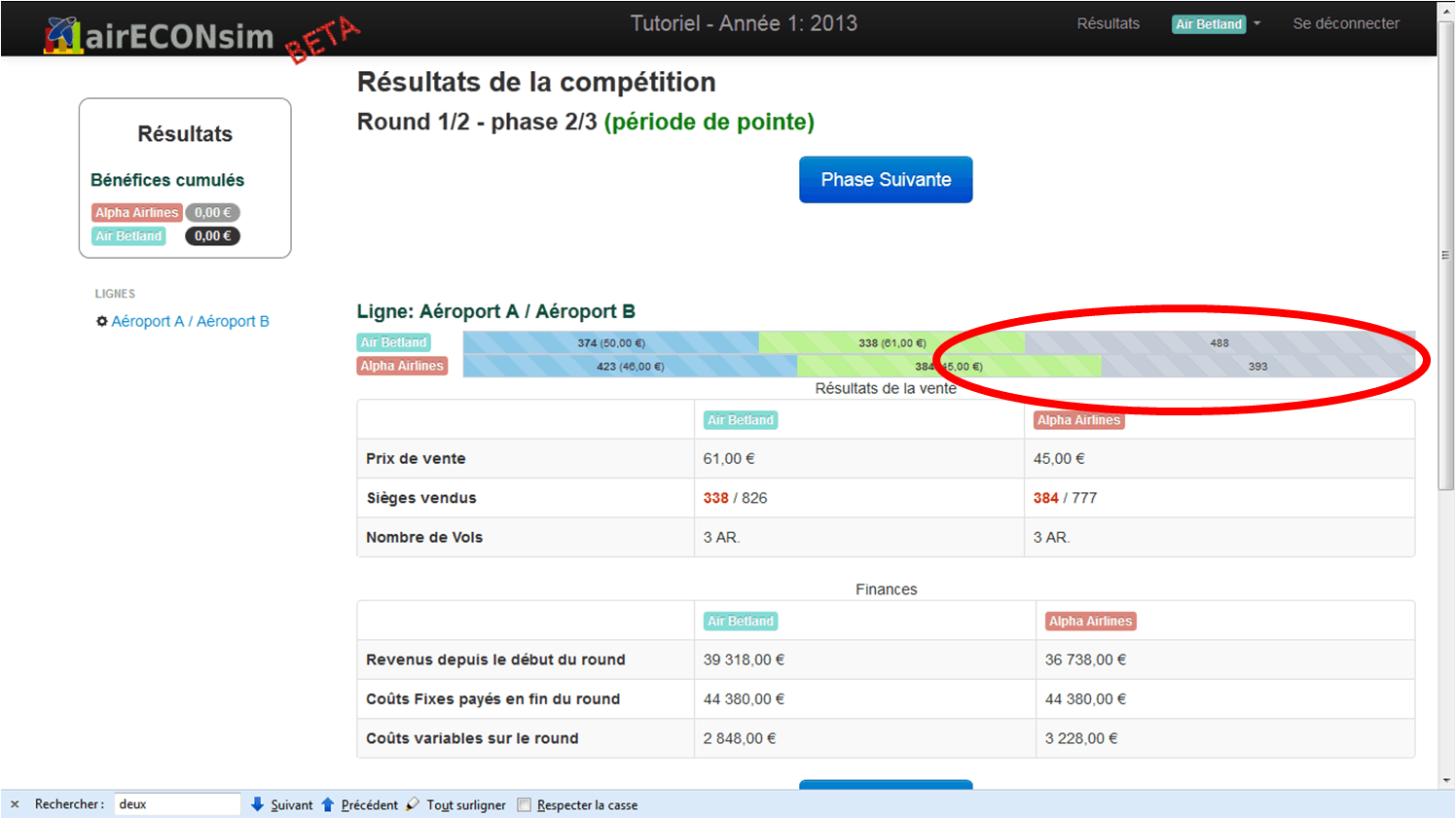
In this picture, the game is at the end of Phase 2. In the bar, you can see the sales and the prices for the first two phases (in color), and the remaining seats for the last phase (in gray, circled in red).

Detailed Years

First Year: Getting to know the game, price elasticity of demand and price discrimination

This Year aims to bring players into the game, quickly and easily. Encourage them not to think too much, the scores will be reset to zero at the beginning of year 2.

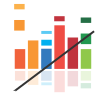
The players are informed that they and their robot-competitor both have 1200 seats to sell for a specific departure date. They also know that the closer they get to departure, the more inelastic demand is, as the proportion of "business" passengers increases.

The cost structure is very simple: €4 per passenger and €48380 of fixed costs per Round (there costs are fixed in the short-run, but become variable in the medium-run, when the player takes control of the number of flights . Cf Year 3).

These costs are calibrated so that the players can not make big profit by keeping their prices constant over the 3 phases. If both competitors keep a price of €50 over all three phases (which is close to the equilibrium price if prices must stay constant), each sells "about" 1070 seats (there are some random shocks in the model). Now, for 1070 seats, the average cost is (4+48380/1070), that is, about € 49.21.

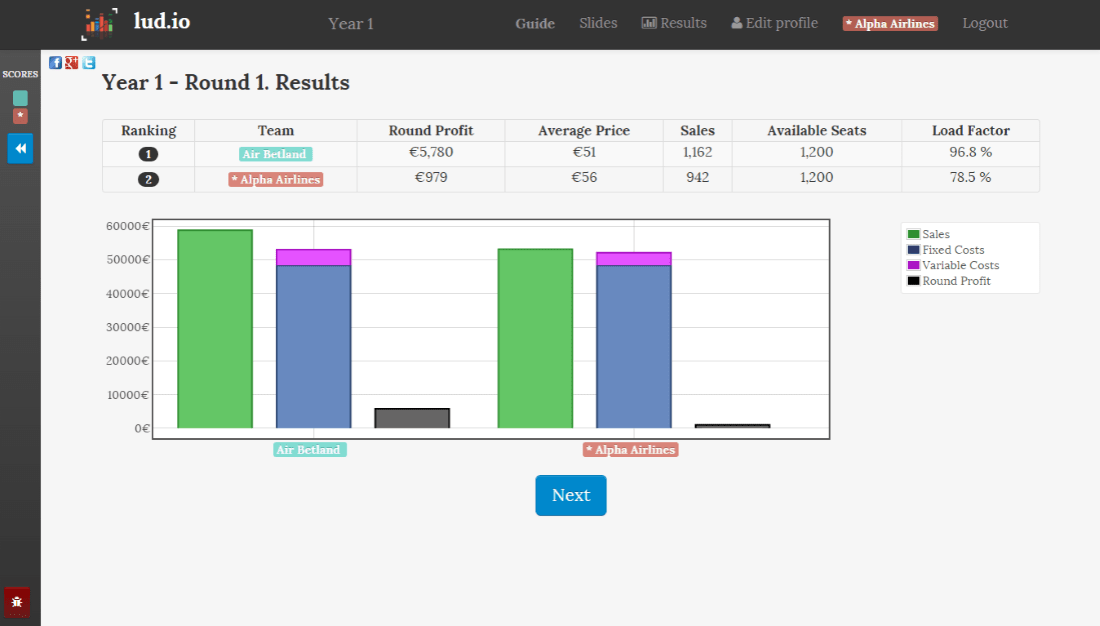
However, if players understand how to use the fact that demand is less elastic when departure gets closer, and implement price discrimination, profit can easily become much more important. From experience, whatever the economics skills of the players, they understand the concept quite easily. A question on one of the transition screens invites them to wonder whether it is possible to increase their average price and still sell as many seats.

During the first Round, the robots just use random prices, but from the second Round, they begin to apply price discrimination (of course, they are not "cheating". Their decisions are not based on players' choices for the current Phase).

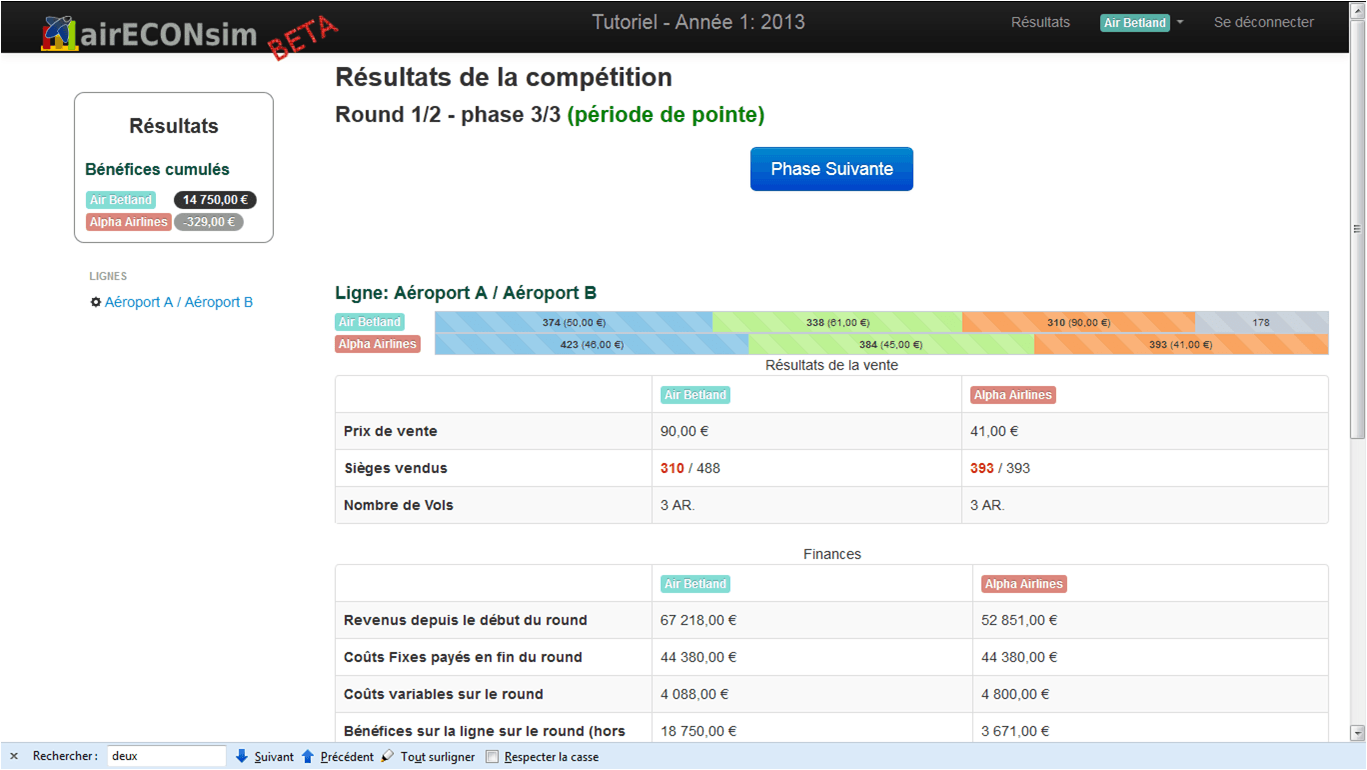
Sometimes, an airline may find itself in a situation of (near) monopoly for the last days before departure, in which case, its profit can explode. This allows to debrief about monopoly and competition.

Second Year: Marginal cost/average cost

Scores are reset to zero, the game really starts.

If you are just running one multiplayer game, all players move forward at the same speed and they do not have the opportunity to go back to change their decisions. In this case, to ensure that no player sinks into negative scores, it may be useful to debrief at the end of the first round and analyze the choices made ​​by the robots. And to invite players to wonder why they are doing better than them, if this is the case (one slide does this).

From this Year, the second round of each year is an off-peak period. Demand is about 2/3 of the "standard" demand.

Just before the start of the off-peak Round, a transition screen tries to trick the players:

First opportunity to warn students against reasonings based on an incorrect analysis of average cost.

Some players, realizing that they have many unsold seats after the first phase of the off-peak round, choose extremely low prices during the last two phases, in a desperate attempt to fill their flights.

This is of course the worst thing to do. As price elasticity of demand is quite low for these last 2 phases, even with a low demand, players should continue to set relatively high prices. Not as high as during the peak period, but they should not drastically cut them. Players who do, get terrible results over the round. This is a good opportunity to highlight that trying to maximize sales at any cost is usually not a good idea, even in situations where unsold products are lost.

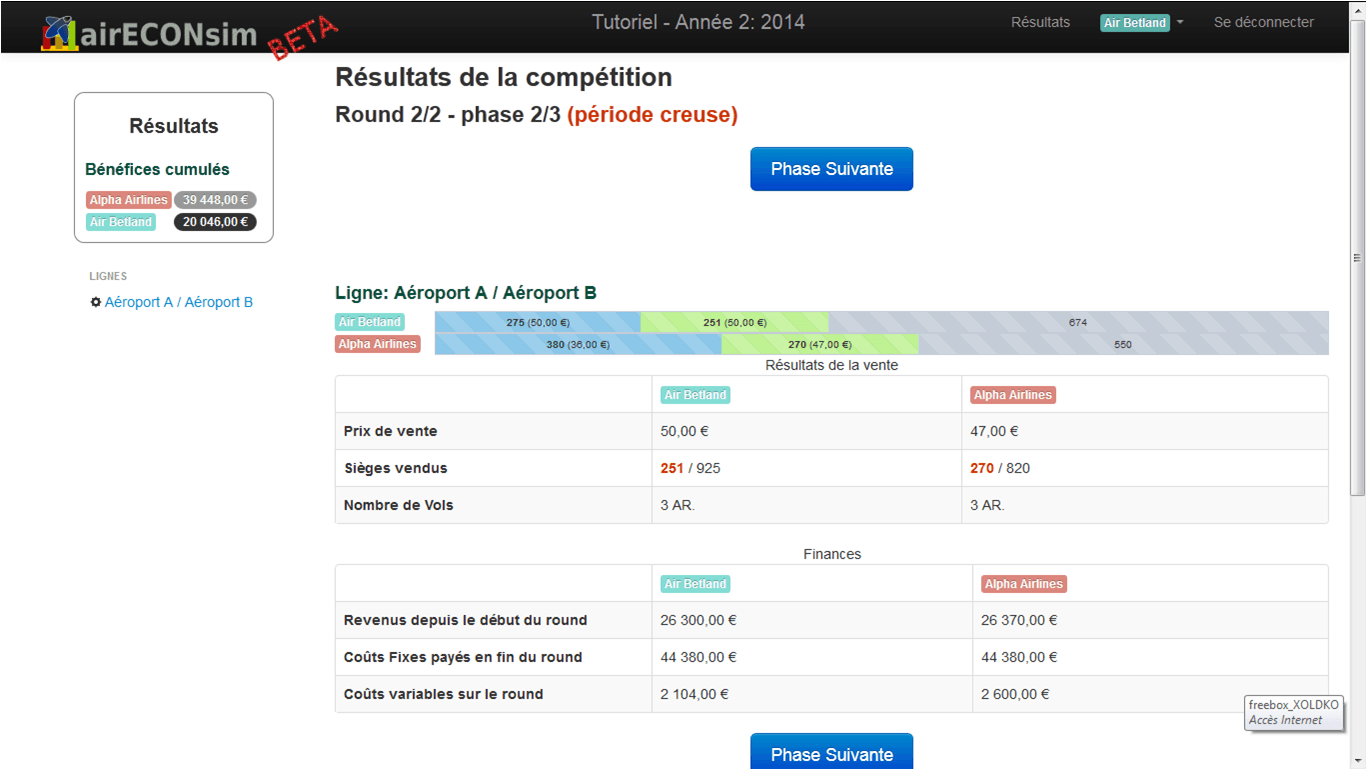
At the end of the second round, players will probably still have empty seats (hopefully, for their profit). The last slide of the year allows to compare once marginal cost and average cost, and to talk about sunk cost:

Third Year: Short-run Cost/Long-run Cost

From the third year, players also control the number of flights on the route.

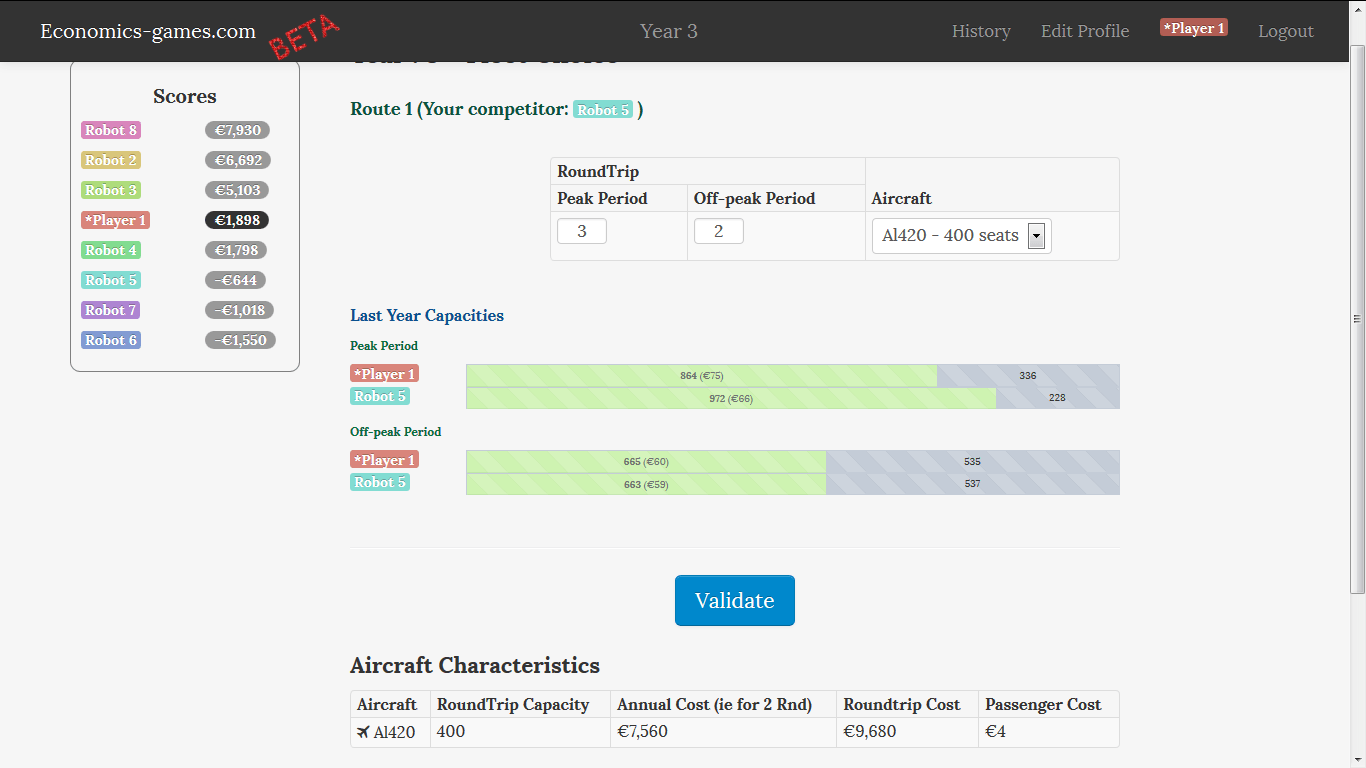
They must choose at beginning of year how many Roundtrips to offer in peak and off-peak periods (considering that one plane can make one Roundtrip during each Round). For example, if they want to operate 2 Roundtrips in the off-peak Round and 5 Roundtrips in the peak Round, they must lease 5 aircrafts throughout the whole year.

Of course, part of the cost is proportional to the number of Roundtrips over the year, and part is proportional to the number of leased planes (ie the number of Roundtrips in peak period).

This new feature allows to discuss many theoretical points, depending on the students' skills.

If students are advanced enough, you can discuss here the principle of peak-load pricing and dimensioning. And once again, emphasize the importance of marginal reasoning (Is it worth leasing an extra plane? If you lease one more plane, will you find an interest in using it in off-peak period or just in peak period? )

It is also an opportunity to present the link between long-run costs and short-run costs. Out of the €48380 that were presented as fixed costs at the beginning of the game, €40380 are in fact the costs incurred for planning 3 Roundtrips in peak periods and 3 Roundtrips in off-peak period. This illustrates how long-run variable costs can become fixed costs in the short-run.

Also, travelers have heterogenous prefered departure times. Departures of the flights are not directly controlled by the players, but this is modeled inside the demand simulation. Consequently, all else being equal (including price), the more flights an airline operates, the more likely it is that one of its flights will be convenient for a given consumer, and eventually, the more seats it will sell. Business passengers value the convenience of departure times more than leisure passengers, so the impact of frequencies on sales is more important in Phase 3 than in Phase 1.

You can, if you wish, introduce the circular city model to your students to illustrate this. You can also mention diminishing returns here, as the effect on sales of adding an extra flight is much more important if you go from one to two flights than if you go from 5 to 6 flights.

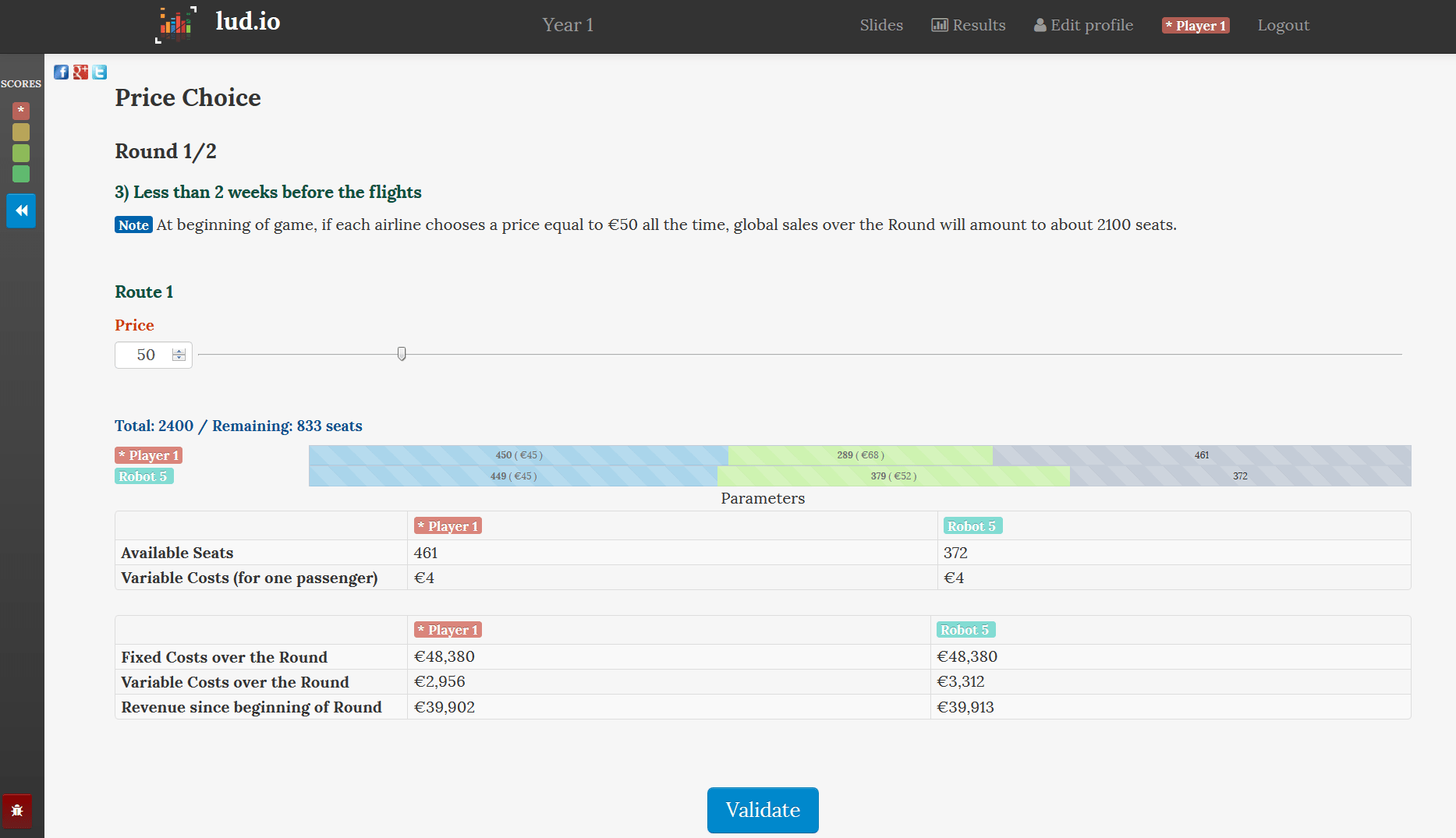
Finally, after a few rounds, your students will realize how the level of production capacity impacts industry profit in the short-run (As illustrated by the graph below: here, the route on which the airlines offer less seats generates the highest total industry profit). You can also use the game to underline that a firm has an incentive to choose a higher production capacity when its competitors have smaller capacities (illustrating this, for example, with a Cournot-like best-reaction curve).

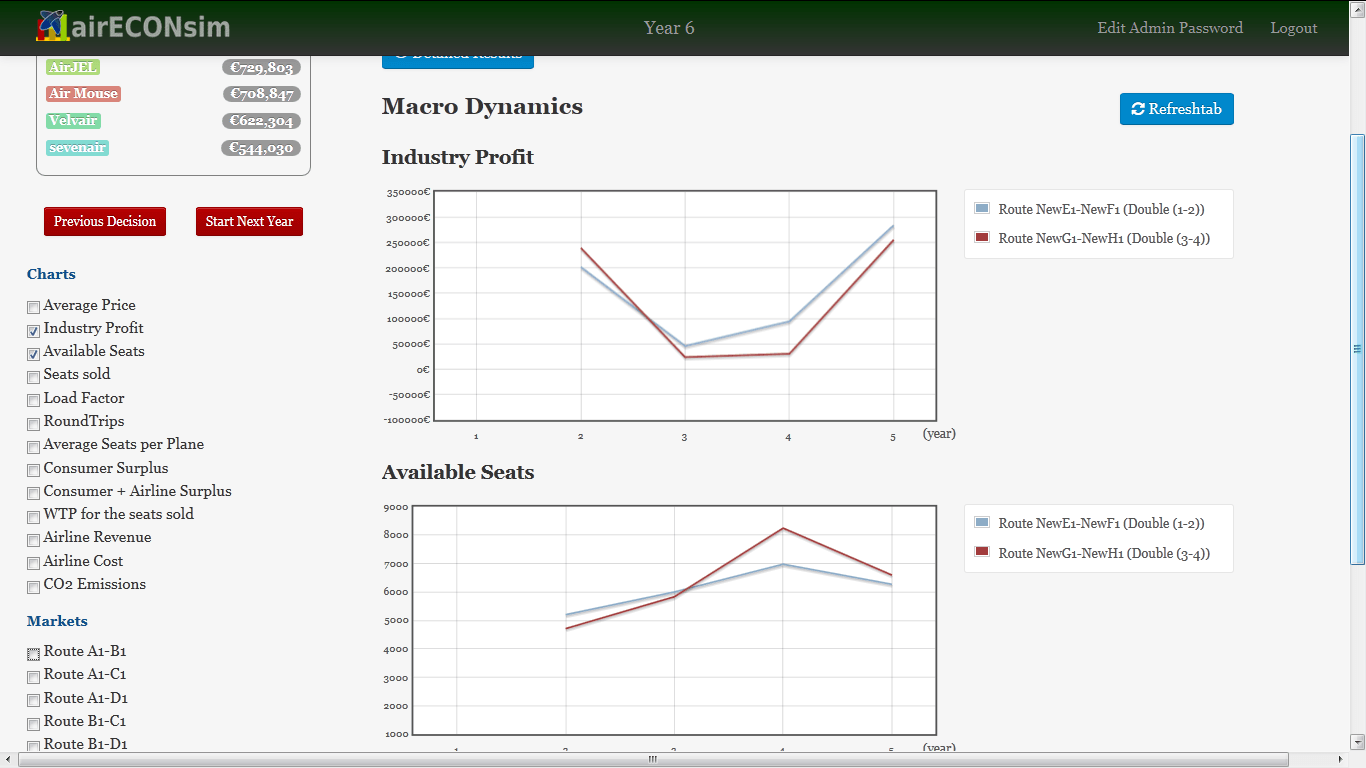
This is a good starting point to debrief (a little later) and discuss the impact of production capacity on the intensity of competition, and possibly present the Cournot model, the logic of competition and the prisoner's dilemma (and Stackelberg, collusion, Kreps-Scheinkman model, ... ).

Fourth Year: Starting to mention differentiation

From the fourth year, players can choose the type of aircraft they use.

The main trade-off: Larger aircraft can reduce the average cost if they are filled (saving on some of the costs, staff, fees, etc.), but involve less frequencies for the same total number of seats. And less frequency means less sales.

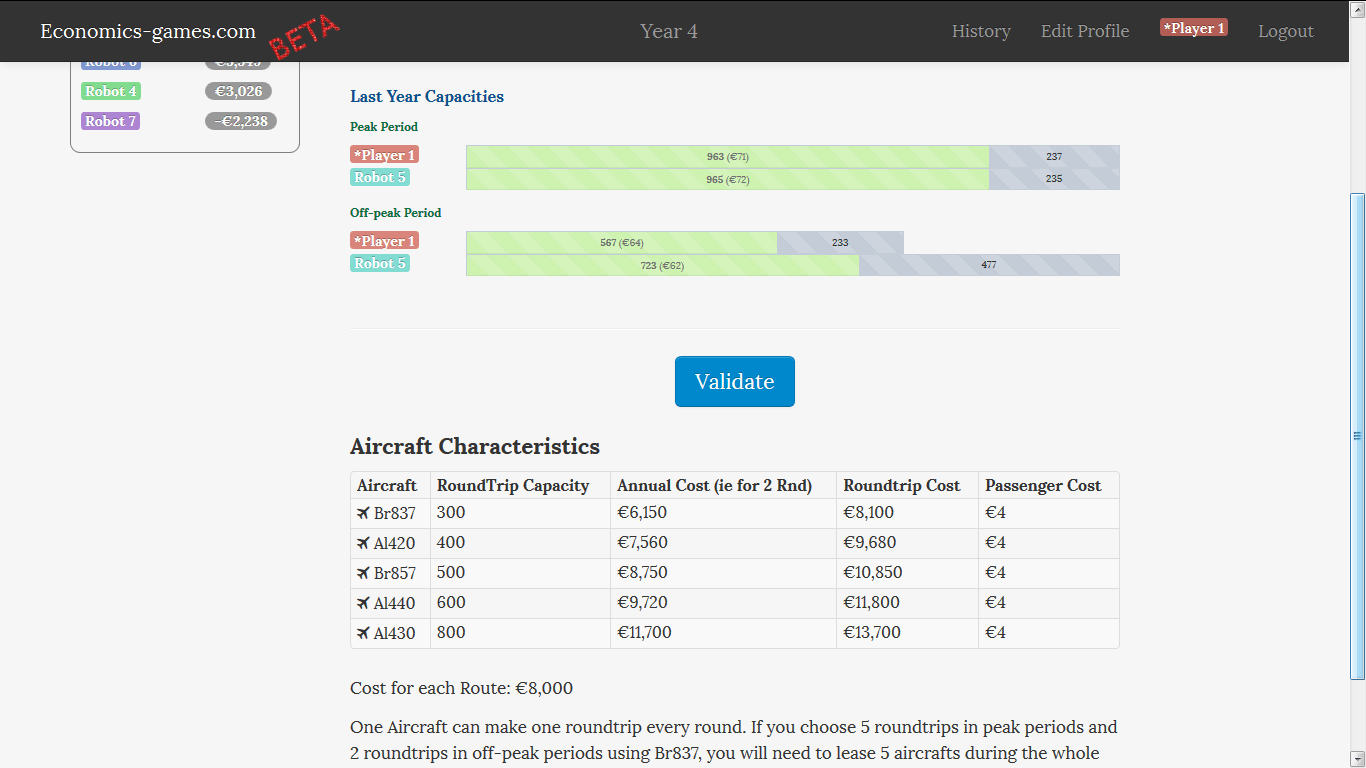
It's up to the players. Above all, this year will be useful to debrief the concepts introduced in year 3.

Fifth and Sixth Years: Vertical Differentiation and end of the game.

In years 5 and 6, the last of the game, players also have the option to install 20% more or less seats in their planes for the same cost. Of course, passengers value comfort, especially business passengers! (and therefore the biggest impact is in Phase 3)

The first slide of the year explains that the players' robot-competitors have made ​​several public statements indicating that they intend to follow a "low cost-related" strategy, and "operate very few flights on large aircraft with the maximum number of seats (which will allow them to sell at very low prices). "

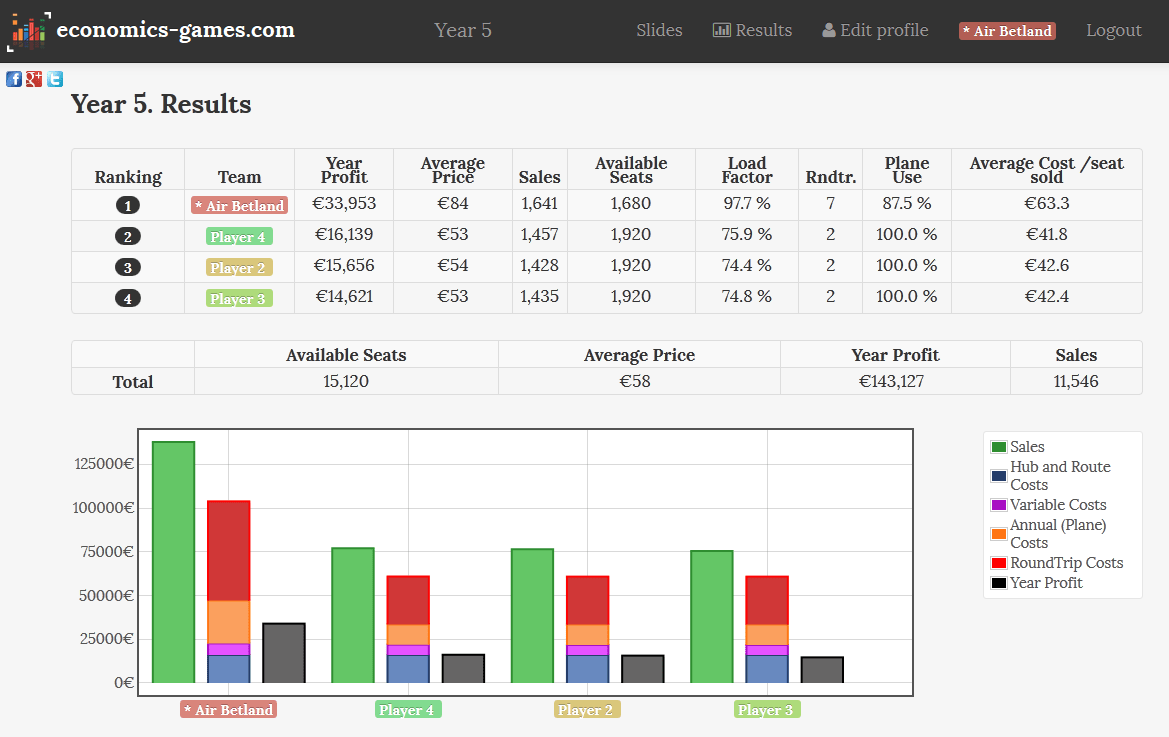
Players have the choice to copy the strategy of their robot-competitors, to differentiate as much as possible by choosing many small planes with very few seats, or to do something in between. Which yields very different results!

Complements

You will find further information about the model of demand in the video below:

This game is a variant of the tutorial of one of our long games (The first four years are exactly the same). You can check its companion document here and adapt it for your students if you wish.