Classroom Games for Teaching Economics
Free, Ready to play, Nothing to install, No need to register!
Students play online on their phones, tablets or laptops.
14 simulations to play alone:
Price discrimination, vertical differentiation and peak-load pricing Top 5! Play
Players take price and quantity decisions for an airline on a given route against a robot competitor. Illustrates notions such as marginal cost/average cost, variable cost/fixed cost, sunk cost, short-run/long-run cost, price discrimination (yield management), elasticity of demand, peak-load pricing...
And eventually, players must choose whether or not to use vertical differentiation to soften competition. This is a classroom variant of the tutorial of our longer industrial organization game.
Also available as a multiplayer game ("Industrial Organization" Section).
Competition Game: Impact of fixed costs and capacity constraints on price and profit, with differentiated goods Top 5! Play
Oligopolistic price competition for differentiated products. Players repeatedly compete on five different markets with only slight differences: with or without unavoidable fixed costs, with or without avoidable fixed costs, with low or high production capacities. Also available as a multiplayer game ("5 IO Market Games" Section).
Competition Game: Price and quantity competition and CO2 environmental policies (quotas, taxes and emission permits) Top 10! Play (vs 5 robots) or Play (as a monopoly)
Impact of environmental policies in a setting with quantity precommitment followed by price competition. Players repeatedly take price and quantity decisions on four markets subject to different environmental policies for CO2 emissions: no policy benchmark, unit taxes, quotas or permits. Also available as a multiplayer game ("5 IO Market Games" Section).
Monopoly Simulation Top 5! oTree Play
The player is a monopoly on a market, and must decide how many goods to produce and what price to set. Marginal and fixed costs change from one round to the other. In round 5, demand gets less elastic.
Perfect Competition Simulation Top 5! oTree Play
The player manages a small firm that competes with many other on a market. From consumers’ perspective, products of all firms are identical. Consumers are also informed about each firm’s price and there are no transportation costs: Consequently, they buy to the firms with the lowest price. The player knows that its competitors’ prices are stable and equal to $180k per unit and must decide what price to set and how much to produce. In round 3, the fixed production cost increases and the player must decide how to react to that.
Horizontal Differentiation Simulation 1 (Linear city with fixed prices) oTree Play
The player is the manager of a store. He is competing with another store in a long, narrow city, with only one street, and must decide where to locate. Customers are uniformly distributed along the street and price is regulated.
Horizontal Differentiation Simulation 2 (Linear city, including price setting) oTree Play
The player is the manager of a store. He is competing with another store in a long, narrow city, with only one street. He must decide where to locate and how to price his products.
2D Hotelling Pricing Game Top 5! oTree Play
You are the manager of a firm, competing with three others to sell a product to the customers of a square country...
Each firm can only be located at a single place, and customers incur quadratic transportation costs when they buy from firms who are not exactly located where they live.
In this game, you can only choose your price: the firms' locations will be given, and will vary from one round to another.
Note that a multiplayer version can also be found in the "Industrial Organization" section.
The Bubble Game (S. Moinas & S. Pouget) Top 10! oTree Play
This game about speculative bubbles "is useful to discuss about market efficiency and trading strategies in a financial economics course, and about behavioral aspects in a game theory course, at all levels"...
"Students sequentially trade an asset which is publicly known to have a fundamental value of zero. If there is no cap on asset prices, speculative bubbles can arise at the Nash equilibrium because no trader is ever sure to be last in the market sequence. Otherwise, the Nash equilibrium involves no trade. Bubbles usually occur with or without a cap on prices. Traders who are less likely to be last and have less steps of reasoning to perform to reach equilibrium are in general more likely to speculate."
Robots' behavior is based on decisions observed in the original scientific experiment.
("The Bubble Game: A Classroom Experiment," Sophie Moinas and Sébastien Pouget, Southern Economic Journal, 2016, vol. 82(4), pages 1402-1412). For advanced students, there exists a very interesting theoretical and experimental extension of this paper: "Learning in Speculative Bubbles: An Experiment" by Hong, Moinas and Pouget.
Note that a multiplayer version can also be found in the "Finance" section.
Can contracts solve the hold-up problem? (E. Hoppe and P. Schmitz) Top 10! oTree Play - 1st treatment (NC) Play - 2nd treatment (FP) Play - 3rd treatment (OC) Play - 4th treatment (OCR)
"How to induce trading partners to make relationship-specific investments is a central theme in the contract-theoretic literature. A party may have insufficient incentives to make non-contractible investments if it fears that it will be held up by its partner in the future...
In this experiment, we consider a buyer and a seller who can trade one unit of an indivisible good at some future date 2.
At date 1, the seller can make a relationship-specific investment e ∈ {el, eh}, which is measured by its costs. In particular, the seller can invest either el = 0€ or eh = 8€. Thereby, the seller influences the buyer’s value from consumption of the good. Depending on the seller’s investment decision, the buyer’s value is either v(el) = 10€ or v(eh) = 22€."
(" Can contracts solve the hold-up problem? Experimental evidence ," Eva I. Hoppe and Patrick W. Schmitz, Games and Economic Behavior, 2011, vol. 73 (1), pages 186-199)
There are 4 different treatments: No contract (NC) / Fixed Price Contract (FP) / The Option Contract (OC) / The Option Contract with Renegotiation (OCR).
In this simulation, you will always be the Seller. The Buyer will be a robot whose behavior is based on decisions observed in the original scientific experiment.
Note that a multiplayer version can also be found in the "Industrial organization" section.
48 multiplayer games:
If you are a player:
If you are an instructor:
Price discrimination, vertical differentiation and peak-load pricing Top 5!
Players take price and quantity decisions for an airline on a given route against a robot competitor. Illustrates notions such as marginal cost/average cost, variable cost/fixed cost, sunk cost, short-run/long-run cost, price discrimination (yield management), elasticity of demand, peak-load pricing...
And eventually, players must choose whether or not to use vertical differentiation to soften competition. This is a classroom variant of the tutorial of our longer industrial organization game.
Warning From lessons learned in recent years, we would recommend that students play the single-player mode of this simulation (located at the top of this page, in the simulations list) rather than this version. It gives them the flexibility to revisit decisions and learn through trial and error, as opposed to being restricted by a shared game's tempo. However, we will still maintain the multiplayer version for instructors who are accustomed to it and might prefer it, based on their experience and judgement.
Stackelberg Game
Each player repeatedly plays two Stackelberg games against the same competitors. Once as a first mover, once as a follower. 2 players on each market and P=20-(Q1+Q2).
Cournot Game
Each player repeatedly plays two cournot games against the same competitors. 2 players on each market and P=20-(Q1+Q2). Preferably, play after the Stackelberg game, so that players get used to the reaction functions.
Bertrand Competition oTree
Players are randomly and anonymously paired with another participant. Each of them represents a firm and sets a price, anything from 0 to 100 points. A buyer in the market buys one unit of the product at the lower price...
Each firm manufactures one unit of the same product at no cost.
When do first-movers have an advantage? A Stackelberg classroom experiment - Cournot (R. Rebelein & E. Turkay) oTree
"The timing of moves can dramatically affect firm profits and market outcomes. When firms choose output quantities, there is a first-mover advantage, and when firms choose prices, there is a second-mover advantage...
Students often find it difficult to understand the differences between these two situations. This classroom experiment simulates each scenario in a way that makes it easy for students to understand the theoretical reasons for the different possible outcomes. The authors have developed a two-firm classroom experiment where students first play a Stackelberg game in which firms sequentially choose production quantities and then a Stackelberg game in which firms sequentially choose prices. When choosing quantities, it is advantageous to move first, and when choosing prices, it is advantageous to wait."
This is the Cournot variant, the Bertrand variant is just below.
("When do first-movers have an advantage? A Stackelberg classroom experiment", Robert Rebelein & Evsen Turkay, Journal of Economic Education 2016)
When do first-movers have an advantage? A Stackelberg classroom experiment - Bertrand (R. Rebelein & E. Turkay) oTree
This is the Bertrand variant of the game presented above...
("When do first-movers have an advantage? A Stackelberg classroom experiment", Robert Rebelein & Evsen Turkay, Journal of Economic Education 2016)
Patents and R&D: A Classroom Experiment (A. Diduch) oTree
"... This classroom experiment provides students with an introduction to two competing models of the impact of patents on R&D: the ‘winner-take-all’ model contains incentives for excessive research effort and the ‘knowledge spillover’model contains incentives for free riding...
Class discussion explores potential changes to current patent policy and policy alternatives for stimulating R&D."
Note: For each patent experiment, a maximum of 5 years is run. If the vaccine has not been found after the 5th year, the game proceeds to the next patent experiment. The first 3 experiments are run without spillovers, the 2 last with spillovers. If you want to skip a patent experiment, you can use the "advance slowest user" of the "monitor" tab of the admin interface.
("Patents and R&D: A Classroom Experiment" by Amy Diduch, IREE 2010)
2D Hotelling Pricing Game Top 5! oTree
Players are managers of a firm that compete with three other firms to sell a product to the customers of a square country...
Each firm can only be located at a single place, and customers incur quadratic transportation costs when they buy from firms who are not exactly located where they live.
In this game, you can only choose your price: the firms' locations will be given, and will vary from one round to another. There is an extended version of this game, just below, in which you can also choose your location.
Note that a single simulation, vs robots, can also be found in the "1-player" section.
2D Hotelling Complete (Pricing and Location) Game oTree
This is the complete variant of the game above...
Before selecting their price, players will be invited to select their location. In the first year, players will have to stay in a pre-allocated quarter. From year 2 on, they will be able to locate everywhere. In year 5 (last year), they can contribute to building a subway which increases customers' demand in the center of the country.
Can Contracts Solve the Hold-Up Problem? (E. Hoppe and P. Schmitz) Top 10! oTree
"How to induce trading partners to make relationship-specific investments is a central theme in the contract-theoretic literature. A party may have insufficient incentives to make non-contractible investments if it fears that it will be held up by its partner in the future...
In this experiment, we consider a buyer and a seller who can trade one unit of an indivisible good at some future date 2.
At date 1, the seller can make a relationship-specific investment e ∈ {el, eh}, which is measured by its costs. In particular, the seller can invest either el = 0€ or eh = 8€. Thereby, the seller influences the buyer’s value from consumption of the good. Depending on the seller’s investment decision, the buyer’s value is either v(el) = 10€ or v(eh) = 22€."
There are 4 different treatments: No contract (NC) / Fixed Price Contract (FP) / The Option Contract (OC) / The Option Contract with Renegotiation (OCR). You can choose the variant when creating the game, and also via the administration interface, inside the game.
Note that a single simulation, vs robots, can also be found in the "1-player" section.
(" Can contracts solve the hold-up problem? Experimental Evidence ," Eva I. Hoppe and Patrick W. Schmitz, Games and Economic Behavior, 2011, vol. 73 (1), pages 186-199)
The Trading Pit Market Experiment oTree
This experiment is used to introduce students to the working of competitive market...
It is based on this document, written for the coreecon textbook by Antonio Cabrales (provides instructions and suggestions). You can also refer to "An Experimental Study of Competitive Market Behavior" (Vernon L. Smith, JPE 1962) and to "Trading in a Pit Market" (Charles A. Holt, JEP 1996).
In the admin interface, you will be able to set a price ceiling and a price floor, along with unit taxes. The players' values are randomly drawn and are displayed on the admin interface.
Logins and passwords for the students will be displayed in a pop-in on top of this page (Warning: You can only connect to one account at a time on the same browser).
Duopoly with Differentiated Demand and Capacity Constraints (B. Çelen & S. Feldmann) oTree
Players are randomly and anonymously paired with another participant, and play 6 rounds of an airline duopoly game with capacity constraints and differentiated demand...
The airlines simultaneously choose capacity and prices with which they compete. The system of demand is linear and symmetric.
You can also find a simulation tool outside of the game: Demand Simulation.
(by Boğaçhan Çelen and Sven Feldmann, Melbourne Business School). Rules and Model of demand.
The Beer Game (J. Sterman) oTree
"The purpose of the game is to understand the distribution side dynamics of a multi-echelon supply chain used to distribute a single item, in this case, cases of beer." The Beer Game, by John Sterman .
Before selecting their price, players will be invited to select their location. In the first year, players will have to stay in a pre-allocated quarter. From year 2 on, they will be able to locate everywhere. In year 5 (last year), they can contribute to building a subway which increases customers' demand in the center of the country.
The 5 market games below can be played on their own or one after the other:
In those games, to allow comparisons, demand on a market is calibrated to be proportional to the number of firms that can be active on it. For example, demand on a market with 6 firms will be 50% more important than on a market with 4 firms. Consequently, potential revenue by firm is the same in each market. (Reference demand data).
Competition Game: Impact of fixed costs and capacity constraints on price and profit, with differentiated goods Top 5!
Oligopolistic price competition for differentiated products. Players repeatedly compete on five different markets with only slight differences: with or without unavoidable fixed costs, with or without avoidable fixed costs, with low or high production capacities.
Warning From lessons learned in recent years, we would recommend that students play the single-player mode of this simulation (located at the top of this page, in the simulations list) rather than this version. It gives them the flexibility to revisit decisions and learn through trial and error, as opposed to being restricted by a shared game's tempo. However, we will still maintain the multiplayer version for instructors who are accustomed to it and might prefer it, based on their experience and judgement.
Introduction to the Competition Games: Sunk costs and monopoly
This is just an introductory variant of the game above, where players are monopolies on their markets and with only two markets (with or without sunk cost, both markets with the same capacity constraints). This is a good introduction to sunk costs and, if played in combination with the game above, it can also be useful to underline differences between monopoly and oligopoly (in these games, demand is proportional to the number of players).
Competition Game: Impact of fixed costs and capacity constraints on price and profit, with homogenous goods
This is the same game as the first competition game except that goods are now homogenous
Competition Game: Impact of the number of competitors on price and profit
Oligopolistic price competition for differentiated products. Players repeatedly compete on two different markets with a different number of competitors (demand is proportional to the number of competitors). Useful to study the impact of the number of firms on competition intensity.
Competition Game: Price and quantity competition and CO2 environmental policies (quotas, taxes and emission permits) Top 10!
Impact of environmental policies in a setting with quantity precommitment followed by price competition. Players repeatedly take price and quantity decisions on four markets subject to different environmental policies for CO2 emissions: no policy benchmark, unit taxes, quotas or permits. Demand is the same as in the other competition games (differentiated demand).
Warning From lessons learned in recent years, we would recommend that students play the single-player mode of this simulation (located at the top of this page, in the simulations list) rather than this version. It gives them the flexibility to revisit decisions and learn through trial and error, as opposed to being restricted by a shared game's tempo. However, we will still maintain the multiplayer version for instructors who are accustomed to it and might prefer it, based on their experience and judgement.
Voluntary contribution to a public good
Each player freely chooses its participation in financing of a pure public good. A player's payoff is equal to twice the average participation minus its individual participation. Repeated Game.
Tragedy of the commons (D. Hazlett) Top 10!
Players jointly own a renewable resource and must make harvesting decisions over a number of periods. This is the classic experiment created by Denise Hazlett ("A Common Property Experiment with a Renewable Resource." Economic Inquiry, 35, October 1997, pp. 858-861), also described in the great site, games economists play (game #75).
Competition Game: Price and quantity competition and CO2 environmental policies (quotas, taxes and emission permits) Top 10!
Impact of environmental policies in a setting with quantity precommitment followed by price competition. Players repeatedly take price and quantity decisions on four markets subject to different environmental policies for CO2 emissions: no policy benchmark, unit taxes, quotas or permits.
Warning From lessons learned in recent years, we would recommend that students play the single-player mode of this simulation (located at the top of this page, in the simulations list) rather than this version. It gives them the flexibility to revisit decisions and learn through trial and error, as opposed to being restricted by a shared game's tempo. However, we will still maintain the multiplayer version for instructors who are accustomed to it and might prefer it, based on their experience and judgement.
The Herd Immunity Game (A. Grant, J. Bruehler & A. Chiritescu) oTree
A particularly potent strain of the flu virus has been discovered in the class, but a vaccine exists. Receiving the vaccination is both painful and expensive for individuals. The more people get vaccinated, the less unvaccinated persons are likely to catch the flu...
("Herd Immunity: A Classroom Experiment," Alan Grant, Jim Bruehler, Andreea Chiritescu, Journal of Economics Teaching, 2016, vol. 1, issue 1, pages 7-16)
Policies with Varying Costs and Benefits: A Land Conservation Classroom Game (S. Dissanayake & S. Jacobson) oTree
This game puts "students in the role of landowners who must decide whether to conserve land in different policy environments: flat conservation payments, agglomeration bonuses, and a conservation auction...
Students learn about specific issues in land conservation, ecosystem services, preferences for nonmoney outcomes, and general issues in policymaking. The game is suited to classes in environmental, resource, agricultural, and policy economics, and more general classes in microeconomics and public policy."
("Policies with Varying Costs and Benefits: A Land Conservation Classroom Game ," by Sahan T. M. Dissanayake and Sarah A. Jacobson, The Journal of Economic Education 2016 47 (2), 142-160)
By default, players locations will randomly change from one round to another, but you can also require that they players at the same place for the whole game. If you select more than one grid, several "subgames" will run at the same time, on comparable grids. For example, if you select 3 grids with 4 rows and 5 columns, the game will involve 3*20=60 players, spread across 3 identical grids.
Logins and passwords for the students will be displayed in a pop-in on top of this page (Warning: You can only connect to one account at a time on the same browser).
The Carbon Trading Game (R. Fouquet) oTree
"A simple game of the market for carbon dioxide tradable permits... As a pedagogical tool, this game benefits from simplicity ... and enables students to grasp the concepts and remember them through the intensity and fun of a trading 'pit'...
The experiences also provide substantial insights into the evolution of the carbon dioxide permit market, particularly related to the evolution of trade volume, permit prices and country strategies."
("The Carbon Trading Game," by Roger Fouquet, Climate Policy 2003 (special Emissions Trading issue), v.3, pp.143-55)
Logins and passwords for the students will be displayed in a pop-in on top of this page (Warning: You can only connect to one account at a time on the same browser).
The Red/Green Simulation (J. Bruehler, A. Grant & L. Ghent) oTree
"Collective action problems are at the heart of many economic issues. Often, students have trouble comprehending how society ends up with a less than optimal outcome, and may incorrectly assume that someone must want the outcome that occurs. Correcting this error is made difficult by the biases that students bring to these issues...
The Red/Green simulation demonstrates the tension between self-interest and the social good in a context-free manner allowing students to see that these sub-optimal outcomes may not be desired by anyone, but instead can result from unhealthy systems of incentives."
("Teaching Collective Action Problems without Contextual Bias: The Red/Green Simulation," by James R. Bruehler, Alan P. Grant, and Linda S. Ghent, Journal of Economics and Finance Education, 2017, Vol. 16 , issue 1)
Logins and passwords for the students will be displayed in a pop-in on top of this page (Warning: You can only connect to one account at a time on the same browser).
Prisoner's Dilemma Top 10!
A repeated Prisoner's Dilemma game.
| Player 1 / Player 2 | Compete | Cooperate |
|---|---|---|
| Compete | 1 , 1 | 5 , -1 |
| Cooperate | -1 , 5 | 3 , 3 |
A n-player Chicken Game
For a project to succeed, a particularly painful task must be undertaken by at least one member of a team. Team members simultaneously choose whether or not to undertake the task. If players behave according to the symetric mixed-strategy nash equilibrium of the game, the more players in the team, the less often the project succeeds. Repeated Game.
Asymmetric Matching Pennies Game
A repeated Asymmetric Zero-Sum Game. A good introduction to Mixed Strategy Nash Equilibria.
| Player 1 / Player 2 | Heads | Tails |
|---|---|---|
| Heads | 5 , -5 | -1 , 1 |
| Tails | -9 , 9 | 5 , -5 |
Battle of the sexes
A standard battle of the sexes game, as described here. Repeated game.
| Player 1 / Player 2 | Prefered Option | Second Option |
|---|---|---|
| Prefered Option | 0 , 0 | 4 , 2 |
| Second Option | 2 , 4 | 0 , 0 |
Simultaneous Entry Game (repeated)
A repeated (simultaneous) Entry Game. Another introduction to Mixed Strategy Nash Equilibria.
| Player 1 / Player 2 | Stay Out | Enter |
|---|---|---|
| Stay Out | 0 , 0 | 0 , 100 |
| Enter | 100 , 0 | -50 , -50 |
The Beauty Contest oTree
Each player will be asked to pick a number between 0 and 100. The winner will be the participant whose number is closest to two-third of the average of all chosen numbers...
The winner will receive 100 points, while other participants will receive nothing. In case of a tie, the 100 points will be equally divided between winners.
Ultimatum Game oTree
Players are randomly and anonymously paired with another participant (depending on your choice when you create the game, pairs will change each round or stay the same). The two participants in a pair will have two different roles: the proposer and the responder. Players will be assigned randomly to a role and will keep it until the end of the game.
Each pair of players will together receive 100 points. The experiment is about how to divide this amount. The proposer will make the responder a take-it-or-leave-it offer, which the responder can accept or reject. If the offer is rejected, both will receive 0 points.
Matching Pennies oTree
Players are randomly and anonymously paired with another participant, and play 10 rounds of "Matching Pennies"...
Player A chooses either "Heads" or "Tails". Player B guesses what Player A chose.
If the guess is correct, Player B receives 100 points and Player A receives nothing. If the guess is incorrect, Player A receives 100 points and Player B receives nothing.
| Player A / Player B | Heads | Tails |
|---|---|---|
| Heads | 0 , 100 | 100 , 0 |
| Tails | 100 , 0 | 0 , 100 |
The Traveler's Dilemma (K. Basu) oTree
Players are randomly and anonymously paired with another participant. Players from each pair are travelers who just returned from a remote island where both of them bought the same antiques. Unfortunately, the airline managed to smash the antiques. The airline manager assures them of adequate compensation. Without knowing the true value of your antiques, he offers players the following scheme...
Players must simultaneously and independently make a claim for the value of their own antique (ranging from 2 points to 100 points):
If both claim the same amount, then this amount will be paid to both. If they claim different amounts, then the lower amount will be paid to both. Additionally, the one with lower claim will receive a reward of 2 points; the one with higher claim will receive a penalty of 2 points.
(Kaushik Basu, "The Traveler's Dilemma: Paradoxes of Rationality in Game Theory"; American Economic Review 1994.)
The Trust Game oTree
Players are randomly and anonymously paired with another participant (depending on your choice when you create the game, pairs will change each round or stay the same). In each pair, one player will be selected at random to be participant A; the other will be participant B. They will keep this role until the end of the game.
To start, participant A receives 100 points, participant B receives nothing. Participant A can send some or all of his 100 points to participant B. Before B receives these points they will be tripled. Once B receives the tripled points he can decide to send some or all of his points to A.
The Bargaining Game oTree
Players are randomly and anonymously paired with another participant. In each pair, there are 100 points for players to divide. They have to simultaneously and independently demand a portion of the 100 points for themselves.
If the sum of demands is smaller or equal to 100 points, both players get what they demanded. If the sum of demands is larger than 100 points, both players get nothing.
The Stag Hunt oTree
Players are randomly and anonymously paired with another participant. Each pair will go for a hunt together. They have the choice of hunting a stag or a hare. If a player chooses to hunt a stag, he can only succeed with the cooperation of the other participant. Players can get a hare by themselves, but a hare is worth less than a stag.
| Player A / Player B | Stag | Hare |
|---|---|---|
| Stag | 200 , 200 | 0 , 100 |
| Hare | 100 , 0 | 100 , 100 |
Customizable Simultaneous Game (2 to 4 actions for each player) oTree
Players are randomly and anonymously paired with another participant, and play up to 10 rounds of a simultaneous game.
The instructor selects the payoffs when creating the game, along with the number of actions for each player (2 to 4)
| Player 1 / Player 2 | A | B |
|---|---|---|
| A | x , x' | y , y' |
| B | z , z' | t , t' |
You can define your own labels for the strategies (with 10 or less alphanumeric characters) or keep the default names (A, B, C or D). Each payoff must be an integer in [-10000 , 10000].
The number of players must be an even number. Logins and passwords for the students will be displayed in a pop-in on top of this page (Warning: You can only connect to one account at a time on the same browser).Customizable 2x2 Sequential Game oTree
Players are randomly and anonymously paired with another participant, and play up to 10 rounds of a sequential game. The instructor selects the payoffs when creating the game.
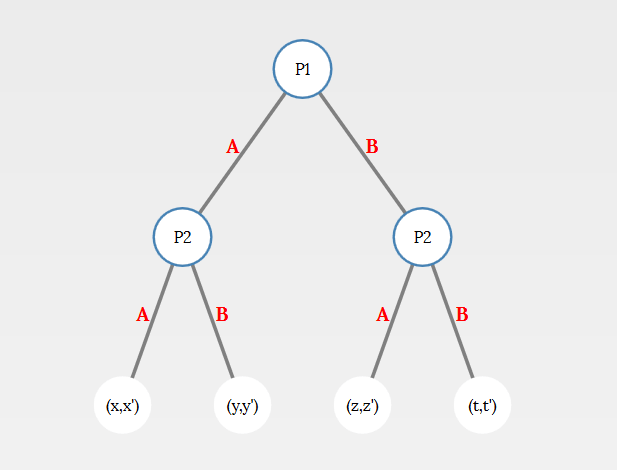
Each payoff must be an integer in [-10000 , 10000].
The number of players must be an even number. Logins and passwords for the students will be displayed in a pop-in on top of this page (Warning: You can only connect to one account at a time on the same browser).Common Value Auction oTree
Players must bid for an item that is being auctioned. Prior to bidding, each player will be given an estimate of the actual value of the item. The estimates may be different between players. The actual value of the item, which is common to all players, will be revealed after the bidding has taken place...
Based on the value estimate, each player will submit a single bid within a given range. All bids are private and submitted at the same time.
The highest bidder will receive the actual value of the item as payoff minus their own bid amount. If the winner's bid amount is higher than the actual value of the item, the payoff will be negative. In the event of a tie between two or more players, the winner will be chosen at random. Other players will receive nothing.
Vickrey Auction oTree
Players are randomly and anonymously matched with another 2 participants in an auction. Each of them is given 100 points to start...
Before bidding, they will learn the value of the object to them. The value of the object differs from participant to participant and is randomly and independently drawn from 0 to 100 for each participant.
In the auction, they will privately submit one bid for the object (anything from 0 to 100 points). The participant with the highest bid wins the object and pays the second highest bid.
The payoff of the winner is calculated as (in points)
Winner’s payoff = 100 + Private value of the object to the winner - Second highest bid
The payoffs for others are the initial 100 points.
The Market for Lemons Game oTree
In this game, players will be grouped randomly and anonymously with another 2 participants (depending on your choice when you create the game, groups will change each round or stay the same). One of them will be randomly assigned to be the buyer and the other 2 will be the sellers (players will keep this role until the end of the game). Sellers and the buyer can trade for 3 periods...
At the beginning of each period, each player will receive 50 points. The sellers will begin by privately choosing a price (from 0 to 50) and a quality grade for their products. Then the buyer will have the chance to purchase from one of the sellers at the price listed. Before purchase, the buyer will not observe grades. After purchase, the price and grade of the bought unit will be revealed to all. The grade can be high, medium, or low; higher grade costs more to produce and is worth more to the buyer. The table below shows production costs to the sellers and values to the buyer of different grades (in points):
| Grade | High | Medium | Low |
|---|---|---|---|
| Production Cost to Sellers | 30 | 20 | 10 |
| Value to the Buyer | 45 | 30 | 15 |
The buyer can buy up to 1 unit of the commodity during a period and each seller can produce up to 1 unit in a period. Unsold units are not produced and hence incur no cost.
The period payoff for the buyer is: Buyer's period payoff = 50 + value of the grade purchased - seller's price
The period payoff for the sellers is: Seller's period payoff = 50 + seller's price - cost of the grade produced
"Design a Contract: A Simple Principal-Agent Problem as a Classroom Experiment" (S. Gächter & M. Königstein) oTree
Players are owners of a firm but lack some expertise to run it and therefore decide to hire experts. They must offer them a contract, consisting of a fixed payment and a proportion of the firm's profit. The experts must then decide whether or not to accept the contract, and if they accept, how much (costly) work effort to make (which determines the total earnings of the firm)...
This experiment "introduces important concepts of organizational economics and incentive contracting. Furthermore, it can also be used to introduce students to the concepts of contractual incompleteness, efficiency, incentive compatibility, outside options and participation constraints, the Coase theorem, and the potential roles of fairness and reciprocity in contracting."
("Design a Contract: A Simple Principal-Agent Problem as a Classroom Experiment", Simon Gächter and Manfred Königstein, Journal of Economic Education 2009, 40, 173–187)
Contracting under Incomplete Information and Social Preferences (E. Hoppe and P. Schmitz) oTree
"We consider a principal who can make a wage offer to an agent for the production of a good. The agent's production costs can be either low or high with equal probability. When the agent accepts the offer, he has to incur the production costs and the principal obtains a return. We consider a setting where the principal's return is larger than the production costs in both states of nature. Hence, ex post efficiency is achieved if the agent accepts the wage offer regardless of the state of nature...
To explore how contracting responds to changes in uncertainty, we have ...four main treatments, using a 2 x 2 design. In particular, we consider two different parameter constellations regarding the agent's production costs and two different information structures. One information structure is relatively simple (the agent always has private information about his production costs from the outset), while the other information structure is more complex (before signing the contract, the agent endogenously decides whether to spend resources to privately learn his production costs)."
(" Contracting under Incomplete Information and Social Preferences: An Experimental Study ," Eva I. Hoppe and Patrick W. Schmitz, Review of Economics Studies, 2013, vol. 80 (4), pages 1516-1544)
There are 4 different treatments: Asymmetric Information with more or less cost dispersion (AI 40-60 and AI 20-80) / Information Gathering with more or less cost dispersion (IG 40-60 and IG 20-80). You can choose the variant when creating the game, and also via the administration interface, inside the game.
The Bubble Game (S. Moinas & S. Pouget) Top 10! oTree
This game about speculative bubbles "is useful to discuss about market efficiency and trading strategies in a financial economics course, and about behavioral aspects in a game theory course, at all levels".
"Students sequentially trade an asset which is publicly known to have a fundamental value of zero. If there is no cap on asset prices, speculative bubbles can arise at the Nash equilibrium because no trader is ever sure to be last in the market sequence. Otherwise, the Nash equilibrium involves no trade. Bubbles usually occur with or without a cap on prices. Traders who are less likely to be last and have less steps of reasoning to perform to reach equilibrium are in general more likely to speculate."
("The bubble game: A classroom experiment," Sophie Moinas and Sébastien Pouget, Southern Economic Journal, 2016, vol. 82(4), pages 1402-1412). For advanced students, there exists a very interesting theoretical and experimental extension of this paper: "Learning in Speculative Bubbles: An Experiment" by Hong, Moinas and Pouget.
Note that a single simulation, vs robots, can also be found in the "1-player" section.
Asymmetric Information Trading Game (B. Biais, D. Hilton, K. Mazurier & S. Pouget) oTree
"... directly inspired by Plott and Sunder (1988). The value of an asset can be high (490), medium (240), or low (50). The traders observe different private signals. For example when the value of the asset is high, half the participants are privately informed that it is not low, while the others learn privately that it not medium.
Traders can place limit and market orders in a call auction and an open outcry continuous market. There is a strong winner’s curse risk in this trading game..."
("Judgemental Overconfidence, Self-Monitoring, and Trading Performance in an Experimental Financial Market," Bruno Biais, Denis Hilton, Karine Mazurier and Sébastien Pouget, 2005, Review of Economic Studies 72, 287–312.)
A Classroom Investment Coordination Experiment. (D.Hazlett) oTree
Players represent firms that make investment decisions. When they expect a recession, their resulting low levels of investment actually cause a recession. Likewise, if they expect an expansion, their resulting high levels of investment can cause an expansion.
"This experiment helps students understand theories that posit coordination failure as the cause of economic fluctuations."
("A Classroom Investment Coordination Experiment", Denise Hazlett, IREE 2007, Volume 6, Issue 1, pp. 63-76, with support from the NSF)
A Classroom Inflation Uncertainty Experiment (D.Hazlett) oTree
"This classroom experiment uses a double oral auction credit market to demonstrate how inflation uncertainty causes a wealth transfer between borrowers and lenders.
The experiment also shows the social cost of inflation uncertainty when borrowers and lenders cannot agree on a nominal interest rate that compensates each for their risk. In this case, the credit market fails to allocate funds to the highest-valued investment projects.
The experiment provides hands-on experience with the effects of anticipated and unanticipated inflation, giving students a common background for a discussion of the economic costs of inflation. It can be used in principles, intermediate macroeconomics,money and banking, or financial economics courses, with 8–60 students..."
("A Classroom Inflation Uncertainty Experiment", by Denise Hazlett, International Review of Economics Education 2008)
For any question or suggestion,