A Repeated Prisoner's Dilemma
Introducing Nash Equilibria and Tacit "Collusion"/Cooperation in repeated games
Rules as explained to players:
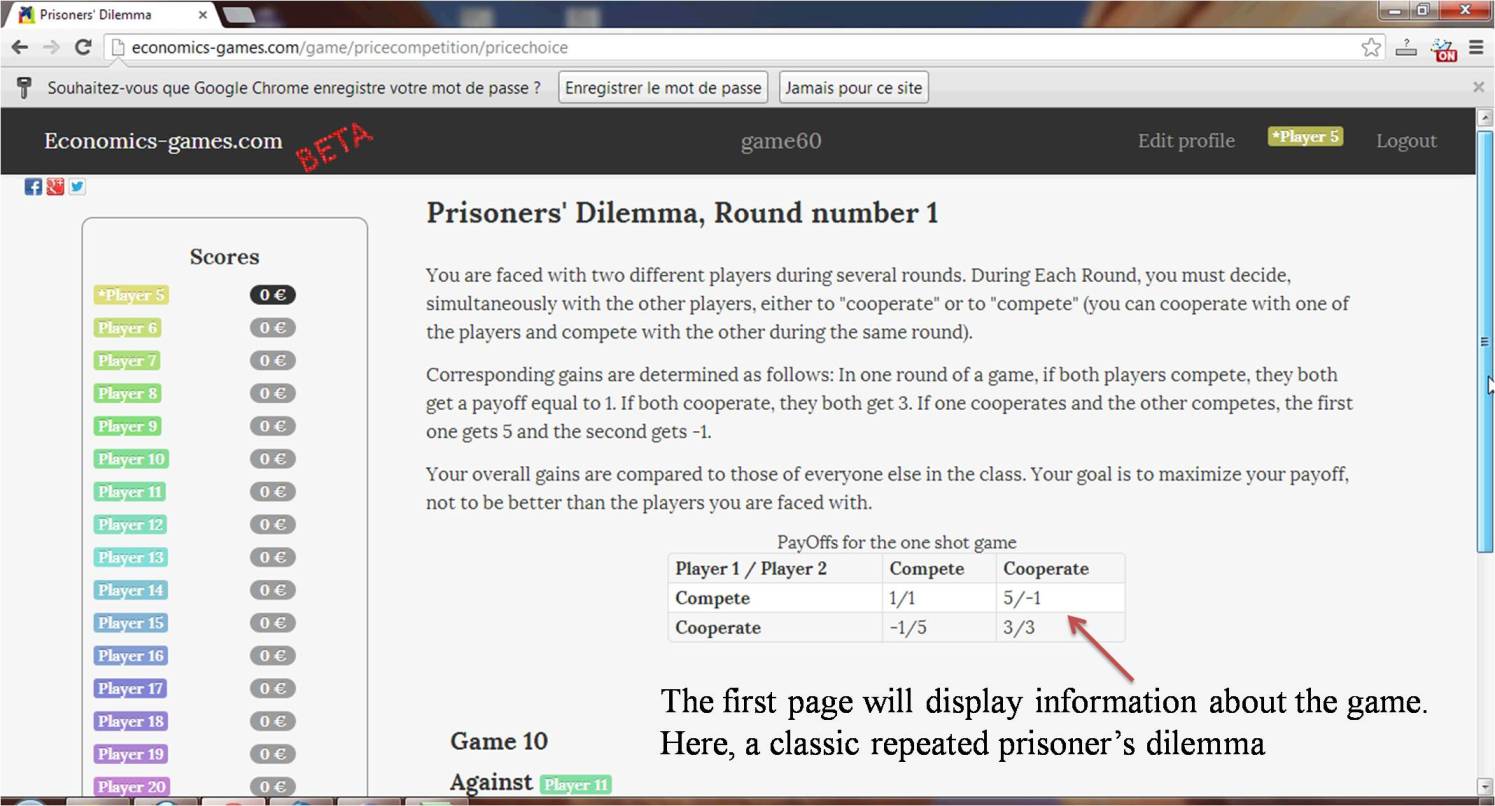
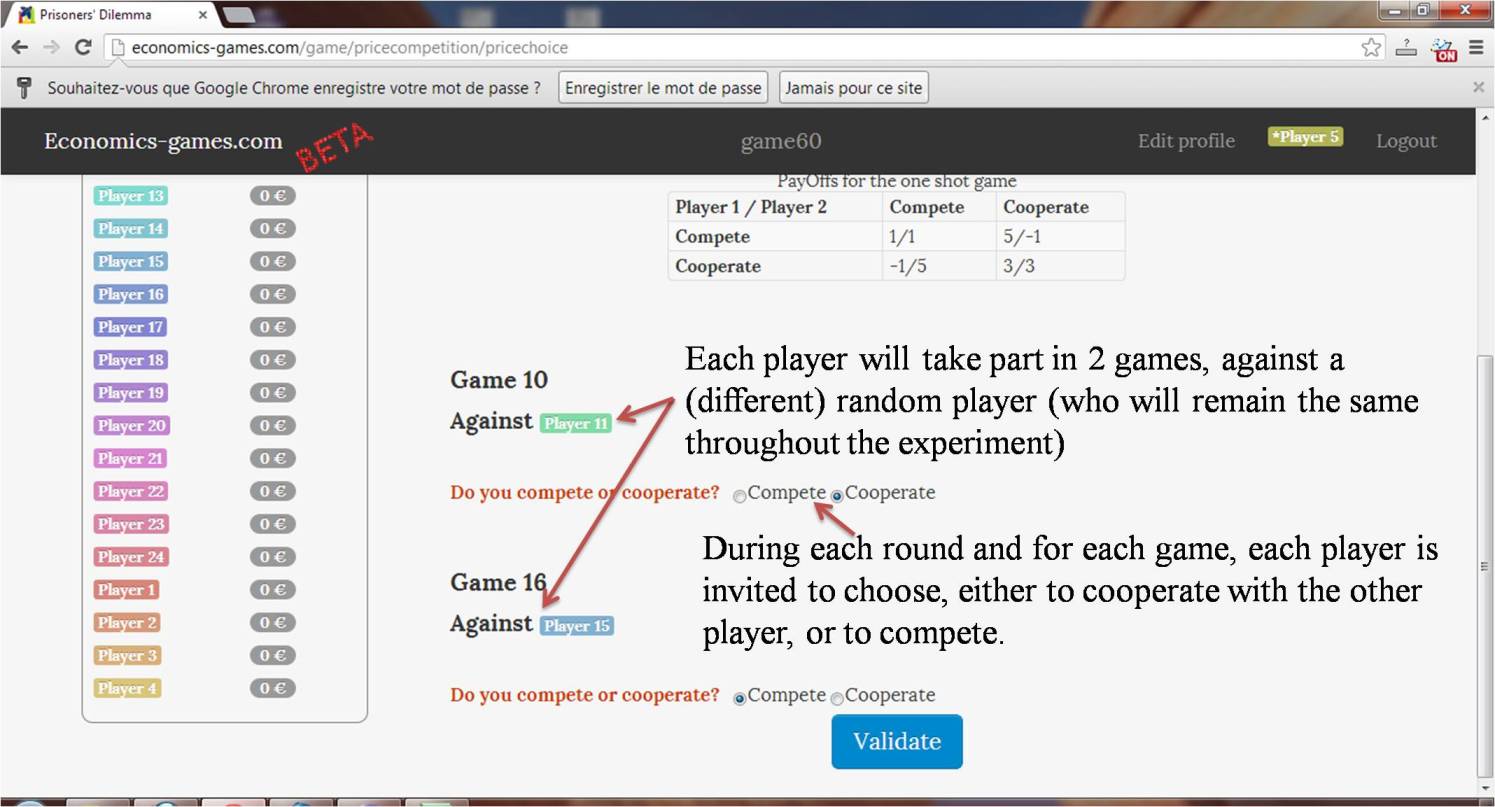
You will play a repeated prisoner's dilemma game repeatedly. In this game, you and another player are firm managers who must decide simultaneously either to "cooperate" or to "compete".
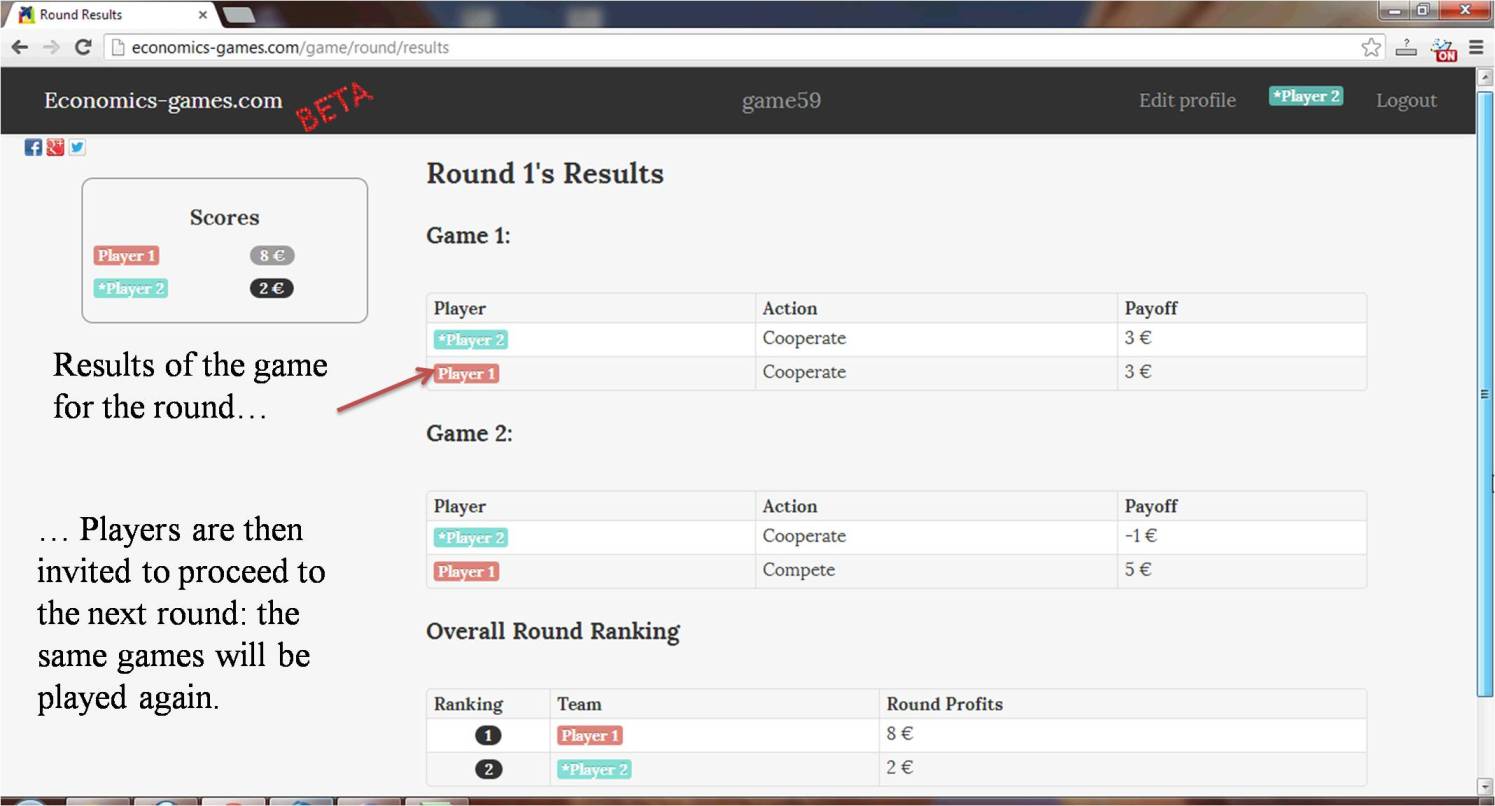
Corresponding payoffs are determined as follows: For one shot of the game, if both players compete, they both get a payoff equal to 1. If both cooperate, they both get 3. If one cooperates and the other competes, the first one gets -1 and the second gets 5.
| Player 1 / Player 2 | Compete | Cooperate |
|---|---|---|
| Compete | 1/1 | 5/-1 |
| Cooperate | -1/5 | 3/3 |
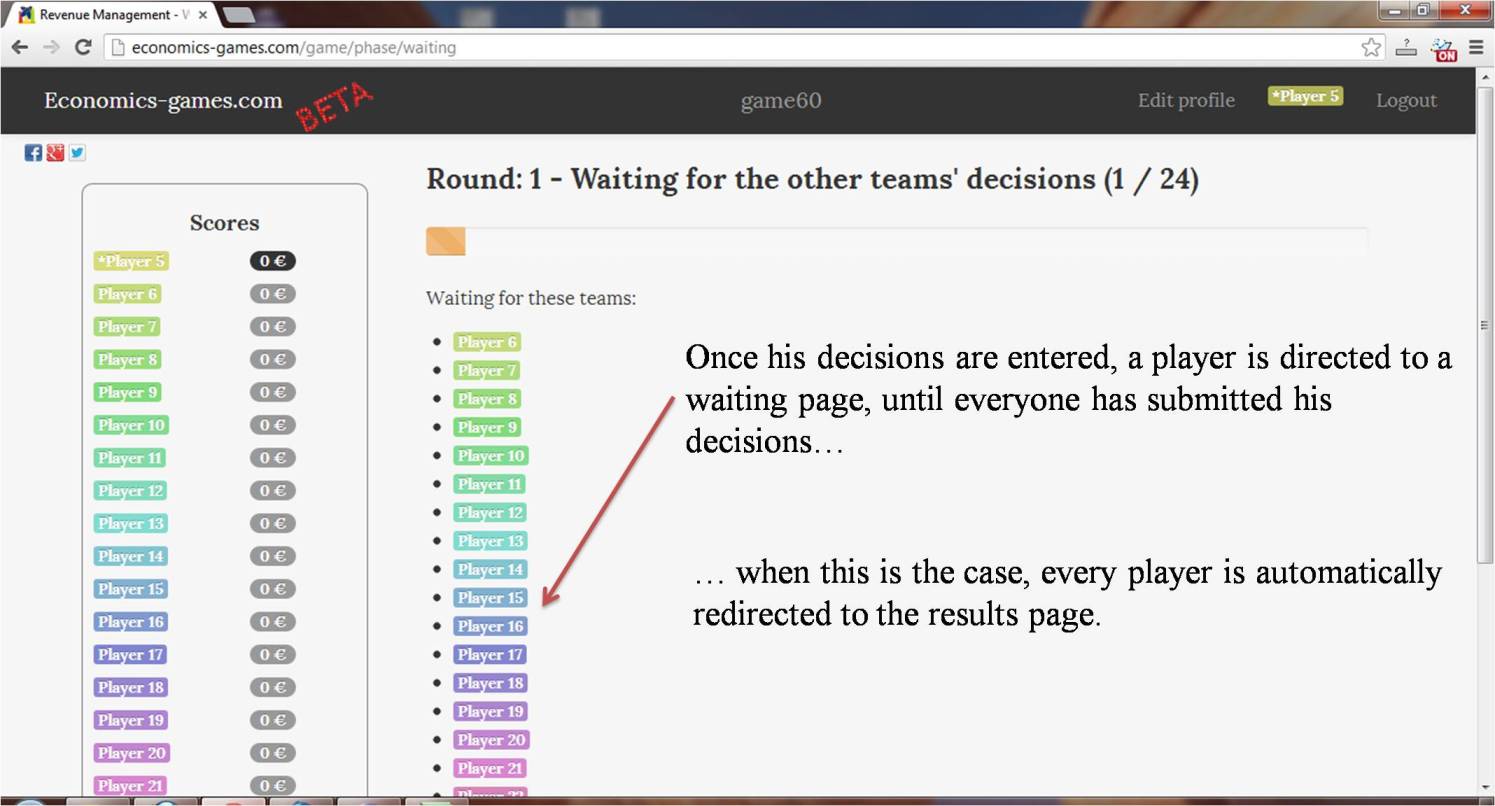
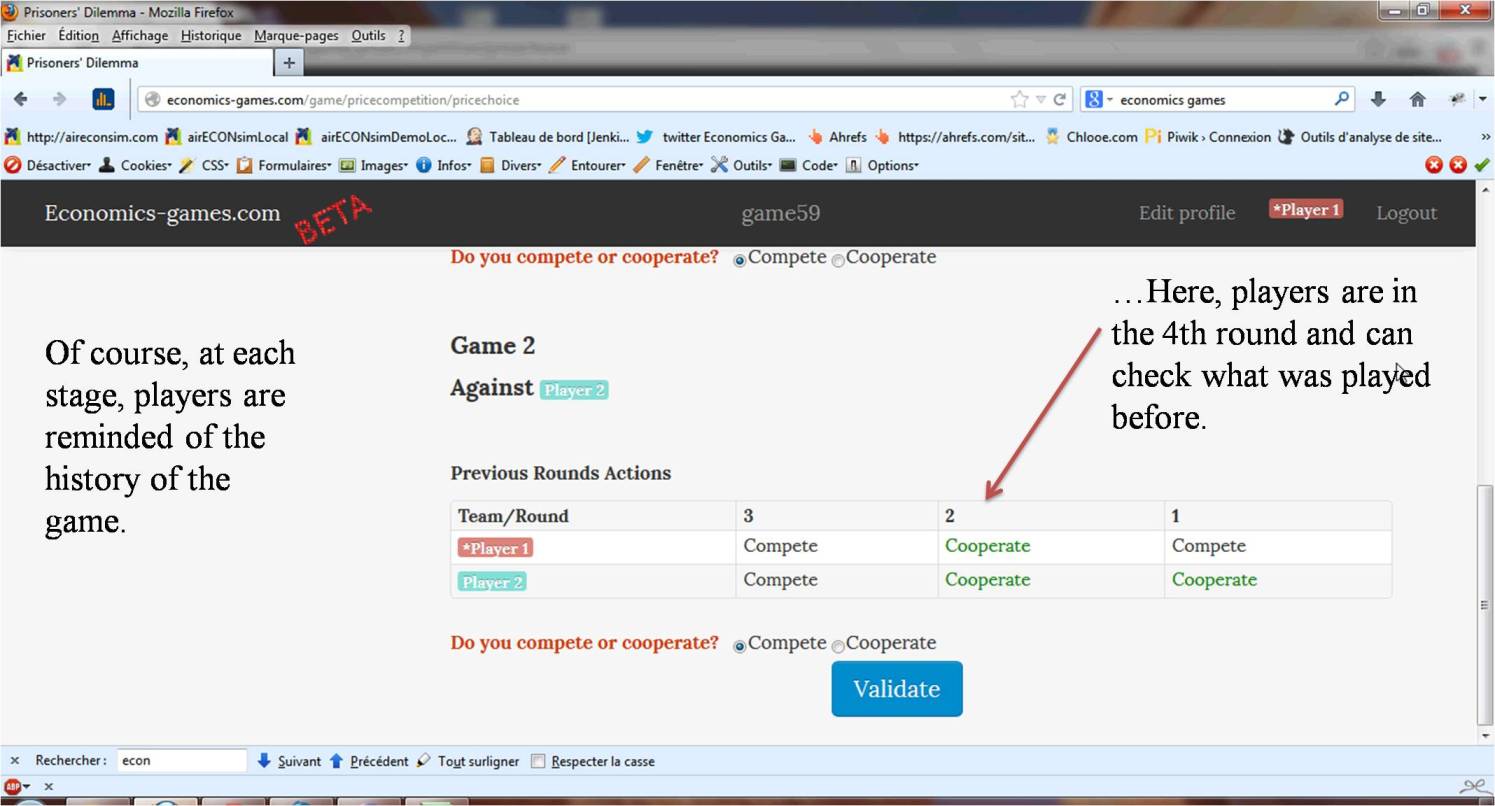
In fact, you will play two of these games at the same time, with random players from your class. You will keep playing with the same two players until the end. So, keep in mind that your action during one round may have some effects on the other player's actions in the next rounds.
Your overall payoffs are compared to those of everyone else in the class. Your goal is to maximize your payoff, not just to be better than the players you are faced with.
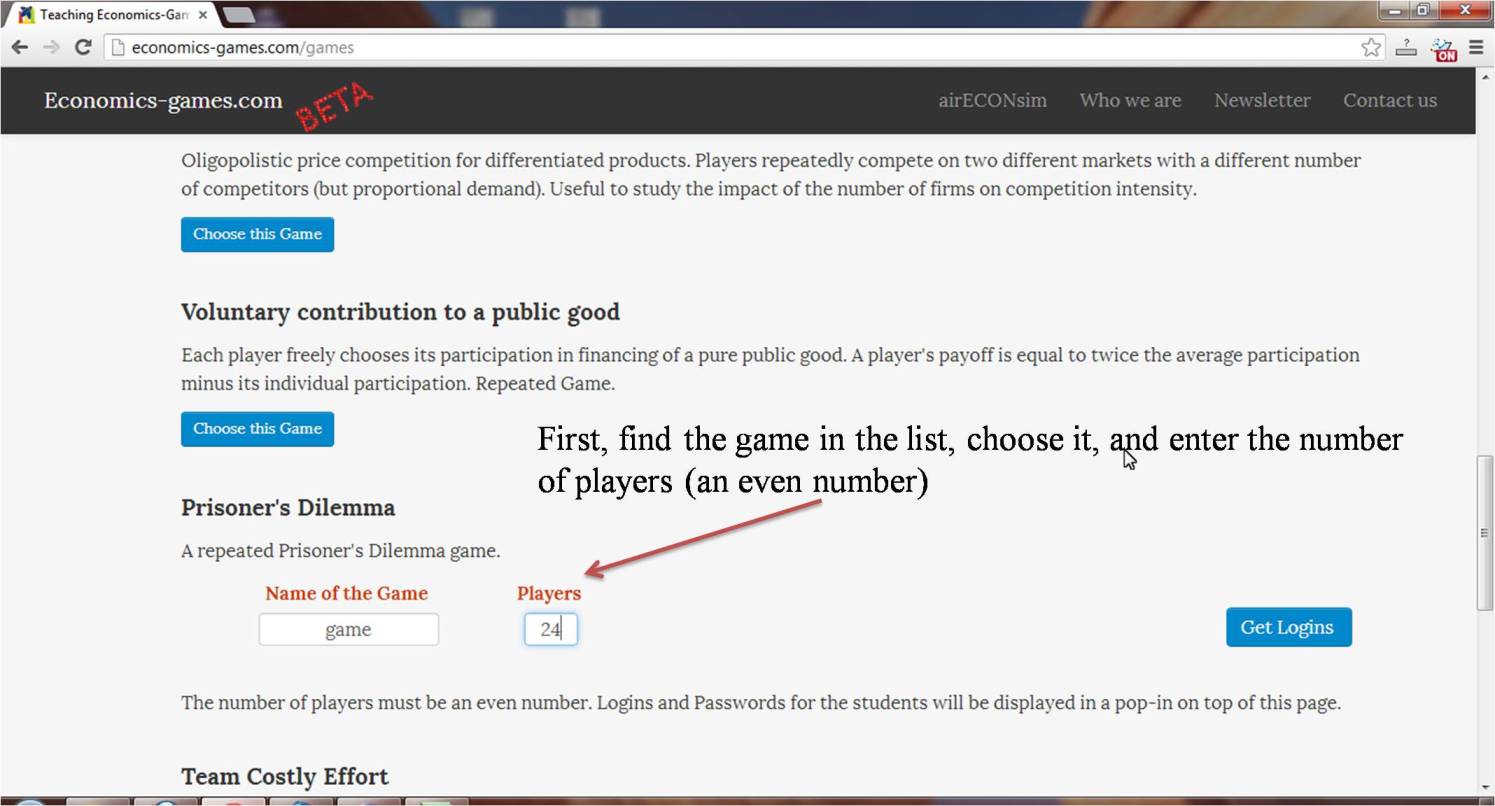
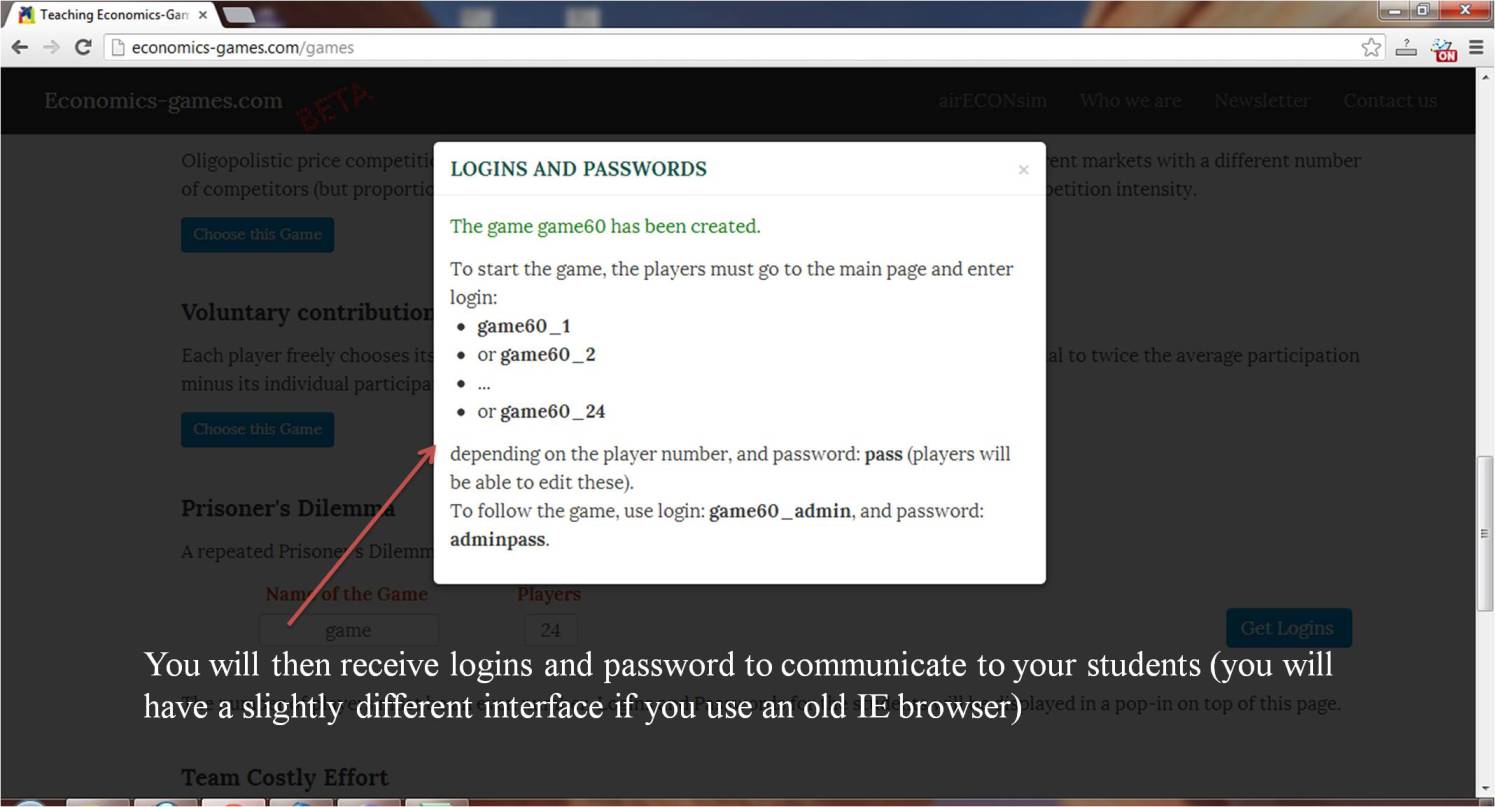
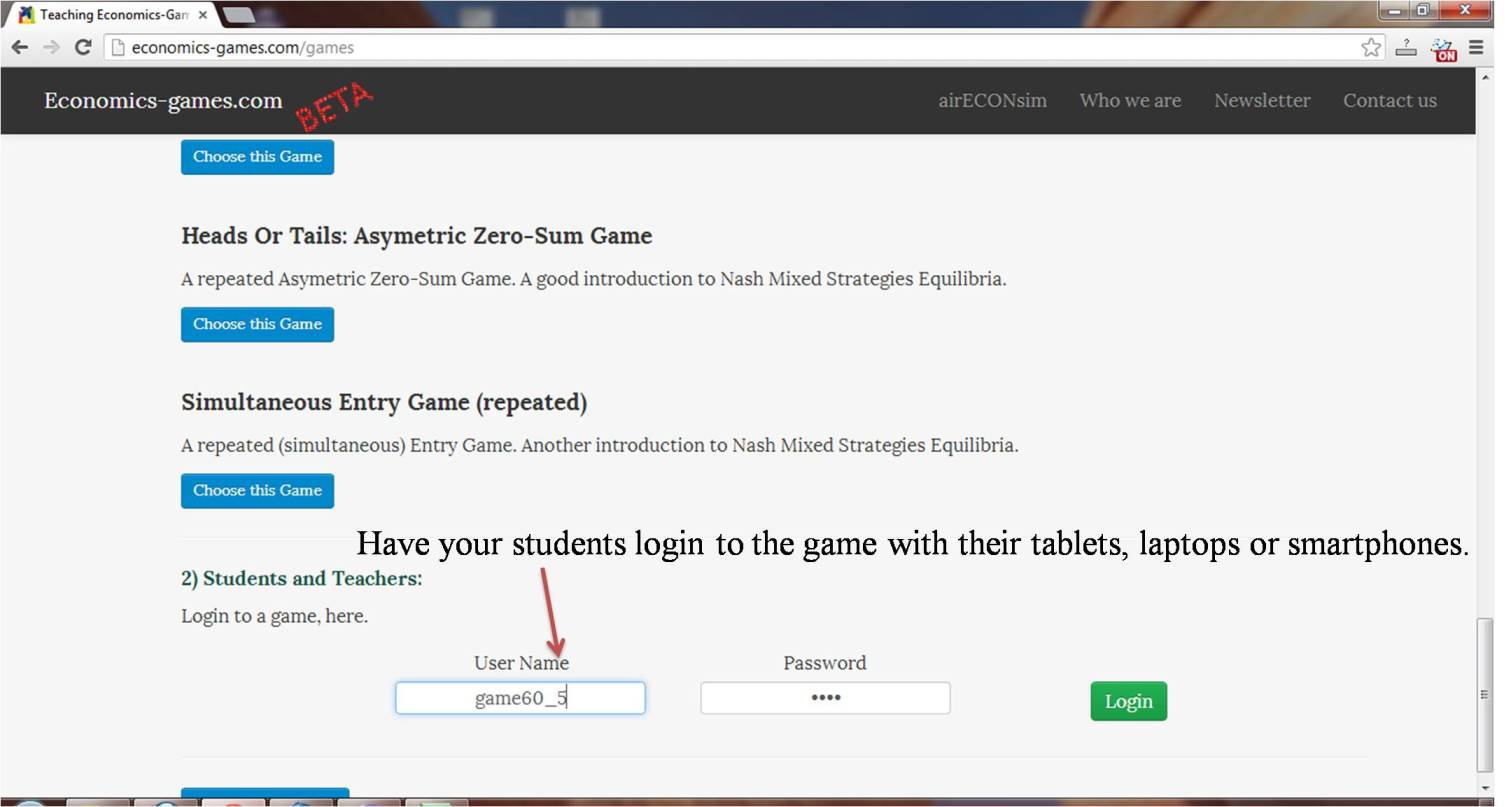
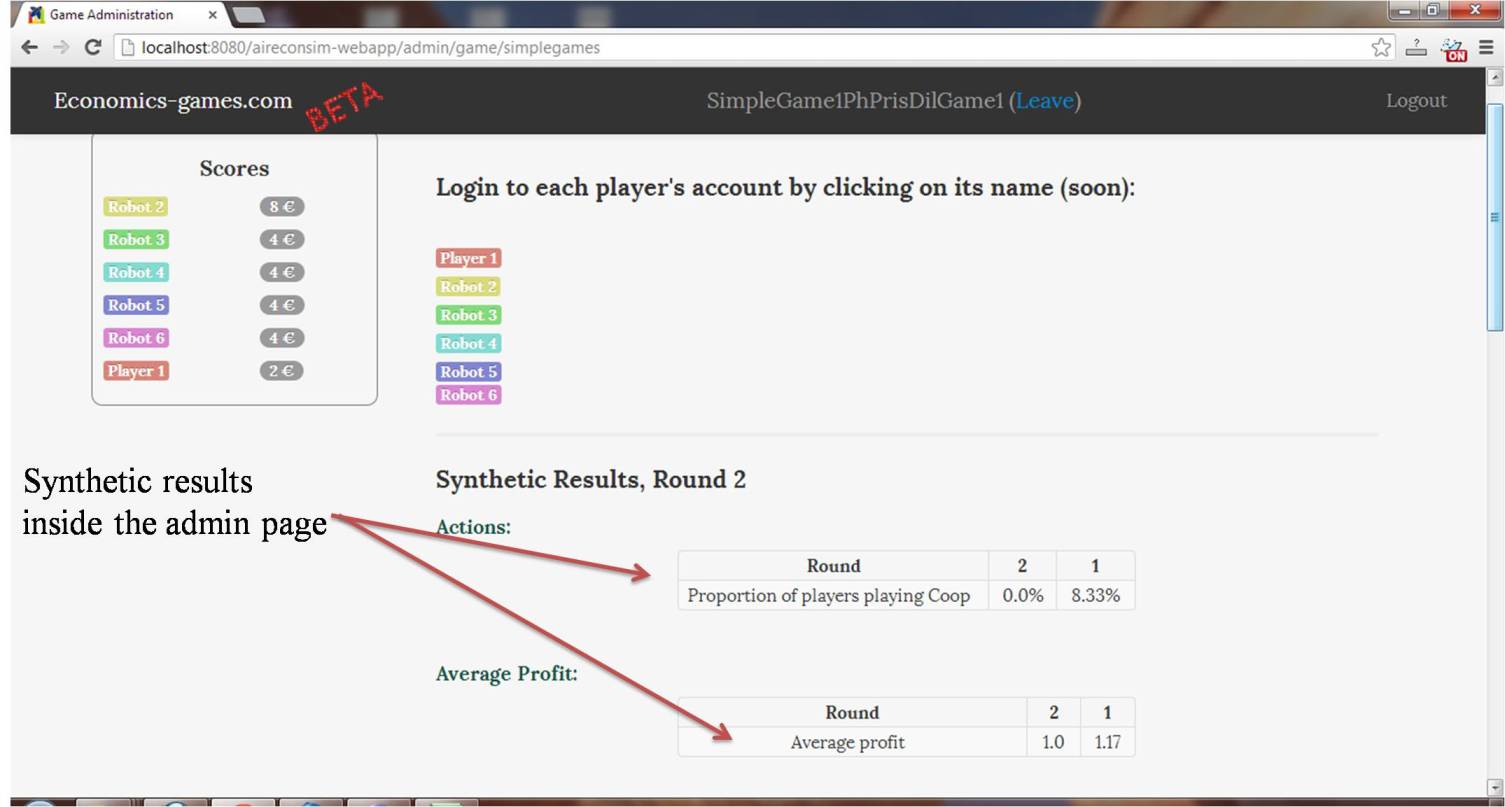
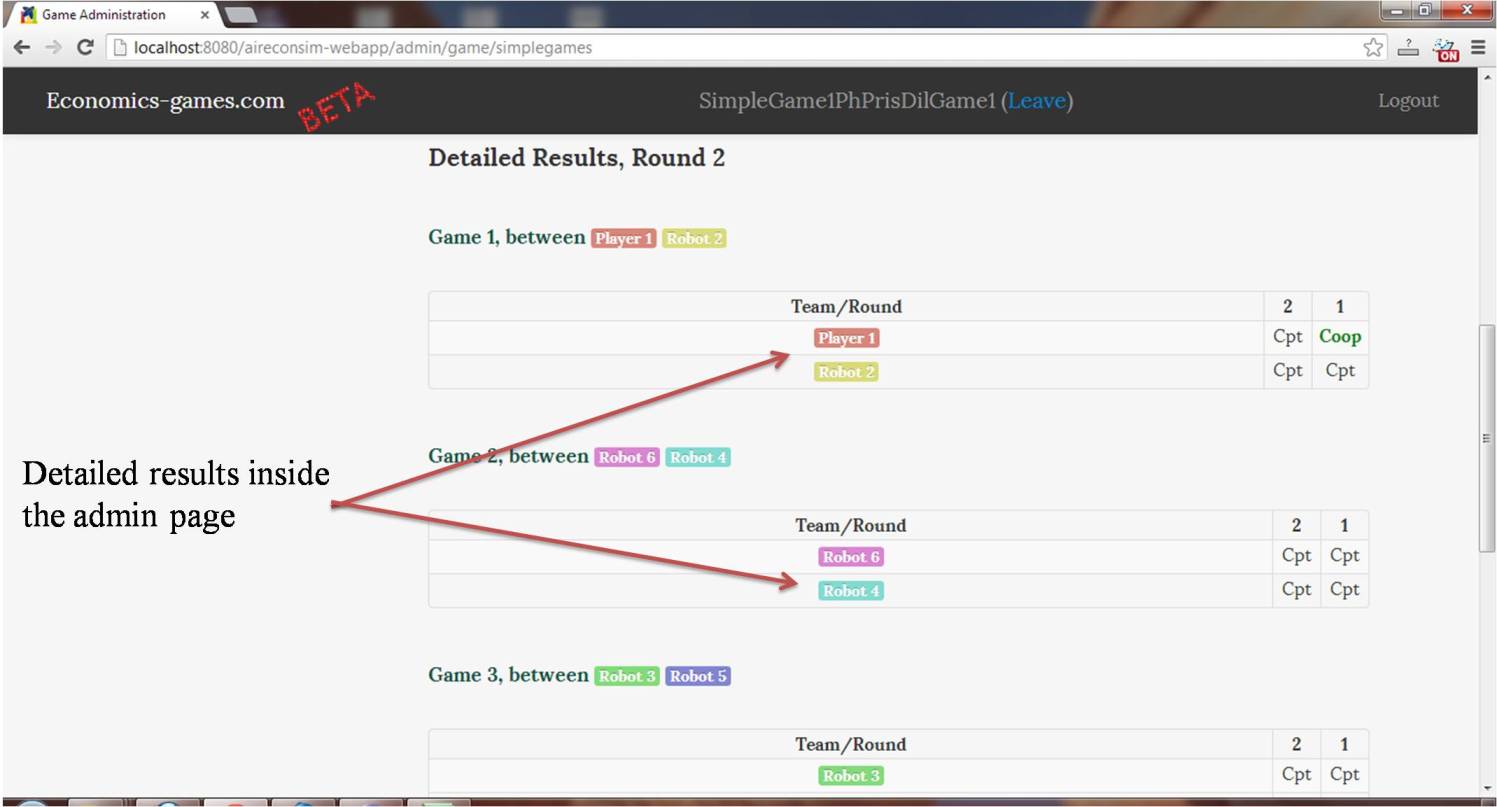
Screenshots and game details: