Jeux pour l'Enseignement de l'Economie
Gratuits, prêt à jouer, rien à installer, pas d'inscription!
Les étudiants jouent en ligne sur leur téléphone, tablette ou portable.
14 jeux à jouer seul.
Jeu de Marché: Impact des coûts fixes et des capacités de production sur les prix et les profits des entreprises (avec biens différenciés)
Top 5!
(  )
Jouer
)
Jouer
Competition en prix pour des biens différenciés. Les joueurs sont en competition sur 5 marchés sur lesquels la demande est identique. Seules la nature des coûts et les capacités de production varient d'un marché à l'autre. Cette simulation est aussi disponible en mode multijoueur (série "5 Jeux de marché").
Discrimination tarifaire, differentiation verticale et tarification de pointe Top 5! Jouer
Les joueurs se voient confier la responsabilité de la gestion de la flotte et de la tarification d'une compagnie aérienne, en concurrence avec une compagnie robot sur une route. Ce jeu permet d'illustrer la différence entre coût moyen et coût marginal, coût fixe et coût variable, coût de long terme et de court terme, ainsi que les notions de coût irrecouvrable, de discrimination tarifaire, d'élasticité-prix de la demande et de tarification de pointe...
A la fin du jeu, les joueurs ont la possibilité d'appliquer une stratégie de différentiation verticale pour diminuer l'intensité de la concurrence. Il s'agit d'une variante "courte" de notre autre jeu, The Airline Game.
Cette simulation est aussi disponible en mode multijoueur (rubrique "Economie Industrielle").
Jeu de Marché: Concurrence en prix et en quantités et politiques environnementales (quotas, taxes et permis d'émission de CO2)
Top 10!
(  )
Jouer (contre 5 robots)
ou
Jouer (en monopole)
)
Jouer (contre 5 robots)
ou
Jouer (en monopole)
Impact des politiques environnementales dans un jeu avec choix de niveau de production suivis par une concurrence en prix. Les joueurs sont en concurrence sur 4 marchés parfaitement isolés soumis à différentes politiques environnementales : un marché de benchmark, un autre avec des taxes unitaires, un avec des quotas et le dernier avec des permis négociables. Cette simulation est aussi disponible en mode multijoueur (série "5 Jeux de marché").
Simulation sur la tarification d'un monopole
Top 5!
oTree
(  )
Jouer
)
Jouer
Le joueur gère une entreprise qui est en situation de monopole sur un marché et doit choisir la quantité de biens à produire et le prix à appliquer. Les coûts changent d'un round à l'autre, ce qui permet de présenter les notions de coût fixe et de coût marginal et de discuter de leur impact sur le prix optimal. Dans le dernier round, c'est la demande qui change, et devient moins élastique.
Simulation: modèle de concurrence pure et parfaite
Top 5!
oTree
(  )
Jouer
)
Jouer
Le joueur gère une petite entreprise qui en concurrence avec de très nombreuses autres (robots) sur un marché. Les consommateurs ne font pas de différence entre les biens des entreprises, sont informés de tous les prix. Par conséquent, ils achètent aux entreprises ayant les prix les plus bas. Le joueur sait que les prix de ses concurrents sont stables et égaux à 180 k$, et doit choisir son prix ainsi que la quantité qu'il souhaite produire. Au round 3, le coût fixe de production augmente et le joueur doit déterminer comment réagir à cette augmentation.
Simulation: modèle de différentiation horizontale 1 (ville linéaire avec prix réglementés)
oTree
(  )
Jouer
)
Jouer
Deux magasins sont en concurrence dans une ville linéaire, pour vendre un produit dont le prix est réglementé. Le joueur doit décider du placement de son magasin.
Simulation: modèle de différentiation horizontale 2 (ville linéaire, avec fixation des prix)
oTree
(  )
Jouer
)
Jouer
Deux magasins sont en concurrence dans une ville linéaire. Le joueur décide du placement de son magasin et du prix de vente de son produit.
Différentiation à la Hotelling, 2D (Tarification)
Top 5!
oTree
(  )
Jouer
)
Jouer
Vous dirigez une entreprise, en concurrence avec 3 autres, sur le marché d'un pays carré...
Chaque entreprise est située en un seul endroit du pays, et ses clients doivent supporter un coût de transport quadratique, fonction de la distance avec leur lieu de vie.
Dans cette simulation, vous ne choisirez que votre prix. Les positions des entreprises seront fixées et varieront d'un tour à l'autre.
Notez qu'une version multijoueur existe, dans la rubrique "Economie Industrielle".
The Bubble Game (S. Moinas & S. Pouget)
Top 10!
oTree
(  )
Jouer
)
Jouer
Ce jeu sur les bulles spéculatives permet de discuter de l'efficience des marchés et des stratégies d'investissement dans un cours d'économie financière...
Les joueurs se revendent séquentiellement un actif, dont la valeur fondamentale est nulle. Si le prix des actifs n'est pas borné, des bulles spéculatives peuvent exister dans un équilibre de Nash, car aucun trader n'est jamais sûr d'être "le dernier à pouvoir acheter l'actif". Dans le cas contraire, l'équilibre de nash implique qu'il n'y a pas d'échanges. En pratique, des bulles sont généralement observées, dans les deux situations.
Les choix des robots sont basés sur les décisions observées lors de l'expérience scientifique.
("The Bubble Game: A Classroom Experiment," Sophie Moinas and Sébastien Pouget, Southern Economic Journal, 2016, vol. 82(4), pages 1402-1412). Il existe une extension théorique et expérimentale de ce papier: "Learning in Speculative Bubbles: An Experiment" par Hong, Moinas et Pouget.
Notez qu'une version multijoueur existe, dans la rubrique "Finance".
Can contracts solve the hold-up problem? (E. Hoppe and P. Schmitz)
Top 10!
oTree
(  )
Jouer - 1er traitement (NC)
Jouer - 2ème traitement (FP)
Jouer - 3ème traitement (OC)
Jouer - 4ème traitement (OCR)
)
Jouer - 1er traitement (NC)
Jouer - 2ème traitement (FP)
Jouer - 3ème traitement (OC)
Jouer - 4ème traitement (OCR)
"How to induce trading partners to make relationship-specific investments is a central theme in the contract-theoretic literature. A party may have insufficient incentives to make non-contractible investments if it fears that it will be held up by its partner in the future...
In this experiment, we consider a buyer and a seller who can trade one unit of an indivisible good at some future date 2.
At date 1, the seller can make a relationship-specific investment e ∈ {el, eh}, which is measured by its costs. In particular, the seller can invest either el = 0€ or eh = 8€. Thereby, the seller influences the buyer’s value from consumption of the good. Depending on the seller’s investment decision, the buyer’s value is either v(el) = 10€ or v(eh) = 22€."
(" Can contracts solve the hold-up problem? Experimental evidence ," Eva I. Hoppe and Patrick W. Schmitz, Games and Economic Behavior, 2011, vol. 73 (1), pages 186-199)
4 traitements différents sont possibles: 'No contract (NC)' / 'Fixed Price Contract (FP)' / 'The Option Contract (OC)' / 'The Option Contract with Renegotiation (OCR)'.
Dans cette simulation, vous aurez toujours le rôle du vendeur. L'acheteur sera un robot calquant son comportement sur ceux observés au cours de l'expérience d'origine.
Notez qu'une version multijoueur existe, dans la rubrique "Economie industrielle".
48 jeux multijoueurs.
Si vous êtes un joueur:
Si vous êtes un enseignant:
Différentiation à la Hotelling, 2D (Tarification)
Top 5!
oTree
(  )
)
Les joueurs dirigent une entreprise, en concurrence avec 3 autres, sur le marché d'un pays carré...
Chaque entreprise est située en un seul endroit du pays, et ses clients doivent supporter un coût de transport quadratique, fonction de la distance avec leur lieu de vie.
Dans cette simulation, vous ne choisirez que votre prix. Les positions des entreprises seront fixées et varieront d'un tour à l'autre. Une version étendue de ce jeu, permettant de choisir sa position, est également disponible, ci-dessous.
Notez qu'une simulation monojoueur (contre robots) existe, dans la rubrique "1 joueur".
Différentiation à la Hotelling, 2D (Localisation et Tarification)
oTree
(  )
)
Il s'agit de la version complète (avec localisation) du jeu présenté ci-dessus...
Avant de choisir leur prix, les joueurs commencent par fixer leur position. La première année, ils doivent rester dans une zone du pays qui leur a été allouée. A partir de l'année 2, ils peuvent se positionner où ils le souhaitent. L'année 5 (dernière année), ils peuvent choisir de contribuer au financement d'un métro qui augmente le nombre de clients présents au centre du pays.
Discrimination tarifaire, differentiation verticale et tarification de pointe Top 5!
Les joueurs se voient confier la responsabilité de la gestion de la flotte et de la tarification d'une compagnie aérienne, en concurrence avec une compagnie robot sur une route. Ce jeu permet d'illustrer la différence entre coût moyen et coût marginal, coût fixe et coût variable, coût de long terme et de court terme, ainsi que les notions de coût irrecouvrable, de discrimination tarifaire, d'élasticité-prix de la demande et de tarification de pointe...
A la fin du jeu, les joueurs ont la possibilité d'appliquer une stratégie de différentiation verticale pour diminuer l'intensité de la concurrence. Il s'agit d'une variante "courte" de notre autre jeu, The Airline Game.
Attention Avec l'expérience de ces dernières années, nous recommandons d'utiliser la simulation monojoueur de ce jeu, contre robots, plutôt que cette version multi-joueur. On peut la trouver dans la liste des simulations, en haut de cette page. Elle est plus pédagogique, car elle permet aux joueurs d'aller à leur rythme, et de revenir en arrière pour modifier leurs décisions et comparer les résultats. Nous laissons quand même l'accès à cette version multi-joueurs pour les enseignants qui ont pris l'habitude de l'utiliser.
Concurrence à la Stackelberg
(  )
)
Chaque joueur participe à deux jeux de Stackelberg (répétés) contre les mêmes concurrents. Une fois comme premier joueur, une fois comme second. 2 joueurs sur chaque marché et P=20-(Q1+Q2).
Concurrence à la Cournot
(  )
)
Chaque joueur participe à deux jeux de Cournot (répétés) contre les mêmes concurrents. 2 joueurs sur chaque marché et P=20-(Q1+Q2). A jouer de préférence après le jeu de Stackelberg, pour que les joueurs soient déjà habitués à la fonction de réaction.
Bertrand Competition
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme. Chacun d'eux représente une entreprise et fixe un prix, entre 0 et 100, pour un produit. Un consommateur achètera une unité du bien le moins cher sur le marché...
Chaque entreprise produit un seul bien homogène sans coût de production.
When do first-movers have an advantage? A Stackelberg classroom experiment - Cournot (R. Rebelein & E. Turkay)
oTree
(  )
)
Dans les modèles de concurrence classiques, une entreprise réalise des profits plus importants si elle joue en premier plutôt que si les choix sont simultanés. Cela ne signifie pas que le premier à choisir a systématiquement un avantage sur les suivants: parfois les profits sont encore plus importants pour les derniers à choisir (par exemple quand la concurrence est en prix)...
Cette expérience permet de comprendre cette distinction, qui est loin d'être évidente. Les auteurs proposent deux variantes: Dans chacune, il y a deux entreprises sur le même marché, et l'une des deux doit choisir son action avant sa concurrente. Dans la première variante, la concurrence est en quantité, dans la seconde, elle est en prix.
Vous pouvez créer ici la version "concurrence en quantité". Pour la version "concurrence en prix", voir le jeu suivant.
("When do first-movers have an advantage? A Stackelberg classroom experiment", Robert Rebelein & Evsen Turkay, Journal of Economic Education 2016)
When do first-movers have an advantage? A Stackelberg classroom experiment - Bertrand (R. Rebelein & E. Turkay)
oTree
(  )
)
Version "concurrence en prix" du jeu présenté ci-dessus...
("When do first-movers have an advantage? A Stackelberg classroom experiment", Robert Rebelein & Evsen Turkay, Journal of Economic Education 2016)
Patents and R&D: A Classroom Experiment (A. Diduch)
oTree
(  )
)
"... This classroom experiment provides students with an introduction to two competing models of the impact of patents on R&D: the ‘winner-take-all’ model contains incentives for excessive research effort and the ‘knowledge spillover’model contains incentives for free riding...
Class discussion explores potential changes to current patent policy and policy alternatives for stimulating R&D."
Note: Pour chaque expérience, on joue un maximum de 5 années. Si le vaccin n'a pas été découvert au bout de la 5ème année, le jeu passe à l'expérience suivante. Les 3 premières expériences sont sans "spillovers", les deux suivantes, avec. Pour sauter une expérience, vous pouvez utiliser le bouton "advance slowest user" de l'onglet "monitor" de l'interface d'administration.
("Patents and R&D: A Classroom Experiment" by Amy Diduch, IREE 2010)
Can Contracts Solve the Hold-Up Problem? (E. Hoppe and P. Schmitz)
Top 10!
oTree
(  )
)
"How to induce trading partners to make relationship-specific investments is a central theme in the contract-theoretic literature. A party may have insufficient incentives to make non-contractible investments if it fears that it will be held up by its partner in the future...
In this experiment, we consider a buyer and a seller who can trade one unit of an indivisible good at some future date 2.
At date 1, the seller can make a relationship-specific investment e ∈ {el, eh}, which is measured by its costs. In particular, the seller can invest either el = 0€ or eh = 8€. Thereby, the seller influences the buyer’s value from consumption of the good. Depending on the seller’s investment decision, the buyer’s value is either v(el) = 10€ or v(eh) = 22€."
4 traitements différents sont possibles: 'No contract (NC)' / 'Fixed Price Contract (FP)' / 'The Option Contract (OC)' / 'The Option Contract with Renegotiation (OCR)'. Vous pouvez choisir la variante à la création du jeu. Vous pourrez aussi la modifier à chaque round dans l'interface d'administration, à l'intérieur du jeu.
Notez qu'une simulation monojoueur (contre robots) existe, dans la rubrique "1 joueur".
(" Can contracts solve the hold-up problem? Experimental Evidence ," Eva I. Hoppe and Patrick W. Schmitz, Games and Economic Behavior, 2011, vol. 73 (1), pages 186-199)
The Trading Pit Market Experiment
oTree
(  )
)
Ce jeu permet de présenter le fonctionnement des marchés concurrentiels...
Il se base sur l'expérience décrite dans ce document, rédigé par Antonio Cabrales pour le manuel coreecon. Vous pouvez aussi consulter les articles "An Experimental Study of Competitive Market Behavior" (Vernon L. Smith, JPE 1962) et "Trading in a Pit Market" (Charles A. Holt, JEP 1996).
Dans l'interface d'administration, vous pourrez choisir un prix plancher et un prix plafond, ainsi que des taxes unitaires. Les valeurs attribuées aux joueurs sont tirées au sort et sont visibles dans l'interface d'administration.
Les Logins and mots de passe apparaîtront dans une fenêtre (Attention: vous ne pouvez vous connecter qu'à un seul compte par navigateur).
Duopole avec demande différenciée et contraintes de capacité. (B. Çelen & S. Feldmann)
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme et jouent 6 rounds de concurrence entre compagnies aériennes...
Ils choisissent simultanément leur prix et la capacité de leur avion. La demande est linéaire et symétrique.
Une simulation est également disponible sur cette page: Simulation de Demande.
(Boğaçhan Çelen and Sven Feldmann, Melbourne Business School). Règles et Modélisation de la Demande.
The Beer Game (J. Sterman)
oTree
(  )
)
"Le but du jeu est de comprendre la dynamique de la distribution d’une chaîne logistique multi-échelons." The Beer Game, par John Sterman .
Avant de choisir leur prix, les joueurs commencent par fixer leur position. La première année, ils doivent rester dans une zone du pays qui leur a été allouée. A partir de l'année 2, ils peuvent se positionner où ils le souhaitent. L'année 5 (dernière année), ils peuvent choisir de contribuer au financement d'un métro qui augmente le nombre de clients présents au centre du pays.
Ces 5 jeux de marchés peuvent être joués seuls ou l'un après l'autre:
Afin de faciliter les comparaisons, la demande a été calibrée pour être proportionnelle au nombre d'entreprises qui sont potentiellement actives sur le marché. Par exemple, la demande sur un marché comportant 6 entreprises est 50% plus importante que sur un marché avec 4 entreprises. Par conséquent, le revenu potentiel par entreprise est le même sur chaque marché. (Données sur la demande de référence).
Jeu de Marché: Impact des coûts fixes et des capacités de production sur les prix et les profits des entreprises (avec biens différenciés)
Top 5!
(  )
)
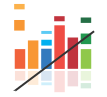
Competition en prix pour des biens différenciés. Les joueurs sont en competition sur 5 marchés sur lesquels la demande est identique. Seules la nature des coûts et les capacités de production varient d'un marché à l'autre.
Attention Avec l'expérience de ces dernières années, nous recommandons d'utiliser la simulation monojoueur de ce jeu, contre robots, plutôt que cette version multi-joueur. On peut la trouver dans la liste des simulations, en haut de cette page. Elle est plus pédagogique, car elle permet aux joueurs d'aller à leur rythme, et de revenir en arrière pour modifier leurs décisions et comparer les résultats. Nous laissons quand même l'accès à cette version multi-joueurs pour les enseignants qui ont pris l'habitude de l'utiliser.
Jeu de Marché: Coûts fixes et Monopole. introduction et préparation au jeu de marché précédent
(  )
)
Ce jeu est juste une variante du jeu précédent, dans laquelle les joueurs sont en monopole sur leur marché. Permet de présenter le plus simplement possible la question de l'impact des coûts fixes irrecouvrables sur les prix. Joué en combinaison avec le jeu précédent (dans lequel la demande est proportionnelle au nombre de joueurs), il permet également de souligner l'impact de la concurrence sur les prix et profits des entreprises.
Jeu de Marché: Impact des coûts fixes et des capacités de production sur les prix et les profits des entreprises (avec biens homogènes)
(  )
)
Même jeu que le premier jeu de marché, mais avec des biens homogènes. Moins réaliste mais convergence vers l'équilibre plus rapide.
Jeu de Marché: Impact du nombre de concurrents sur les prix et profits
(  )
)
Concurrence en prix avec des biens différenciés. Les joueurs sont actifs sur deux marchés, un gros marché avec de nombreux concurrents et un petit marché avec peu de concurrents. La demande est proportionnelle au nombre de concurrents. Jeu utile pour illustrer l'impact du nombre de concurrents sur l'intensité de la concurrence.
Jeu de Marché: Concurrence en prix et en quantités et politiques environnementales (quotas, taxes et permis d'émission de CO2)
Top 10!
(  )
)
Impact des politiques environnementales dans un jeu avec choix de niveau de production suivis par une concurrence en prix. Les joueurs sont en concurrence sur 4 marchés parfaitement isolés soumis à différentes politiques environnementales : un marché de benchmark, un autre avec des taxes unitaires, un avec des quotas et le dernier avec des permis négociables. La demande est la même que dans les autres jeux de marché de ce site (demande différenciée).
Attention Avec l'expérience de ces dernières années, nous recommandons d'utiliser la simulation monojoueur de ce jeu, contre robots, plutôt que cette version multi-joueur. On peut la trouver dans la liste des simulations, en haut de cette page. Elle est plus pédagogique, car elle permet aux joueurs d'aller à leur rythme, et de revenir en arrière pour modifier leurs décisions et comparer les résultats. Nous laissons quand même l'accès à cette version multi-joueurs pour les enseignants qui ont pris l'habitude de l'utiliser.
Financement volontaire d'un bien public et passager clandestin.
(  )
)
Les joueurs doivent décider simultanément de leur contribution au financement d'un bien public pur. Le "gain" d'un joueur est égal à deux fois la moyenne des contributions moins sa propre contribution. Il s'agit d'un jeu répété.
Tragédie des biens communs (D. Hazlett)
Top 10!
(  )
)
Les joueurs sont ont un accès commun à une ressource renouvelable et doivent décider de la vitesse à laquelle ils l'exploitent sur plusieurs périodes . Il s'agit de l'expérience classique créée par Denise Hazlett ("A Common Property Experiment with a Renewable Resource." Economic Inquiry, 35, October 1997, pp. 858-861), qui est également décrite sur le très bon site, games economists play (jeu #75).
Jeu de Marché: Concurrence en prix et en quantités et politiques environnementales (quotas, taxes et permis d'émission de CO2)
Top 10!
(  )
)
Impact des politiques environnementales dans un jeu avec choix de niveau de production suivis par une concurrence en prix. Les joueurs sont en concurrence sur 4 marchés parfaitement isolés soumis à différentes politiques environnementales : un marché de benchmark, un autre avec des taxes unitaires, un avec des quotas et le dernier avec des permis négociables.
Attention Avec l'expérience de ces dernières années, nous recommandons d'utiliser la simulation monojoueur de ce jeu, contre robots, plutôt que cette version multi-joueur. On peut la trouver dans la liste des simulations, en haut de cette page. Elle est plus pédagogique, car elle permet aux joueurs d'aller à leur rythme, et de revenir en arrière pour modifier leurs décisions et comparer les résultats. Nous laissons quand même l'accès à cette version multi-joueurs pour les enseignants qui ont pris l'habitude de l'utiliser.
The Herd Immunity Game (A. Grant, J. Bruehler & A. Chiritescu)
oTree
(  )
)
Un nouveau virus de grippe particulièrement virulent se répand dans la classe, mais un vaccin existe. Se faire vacciner est à la fois douloureux et cher. Plus il y a vaccinés, moins les joueurs non vaccinés risquent d'attraper la grippe...
("Herd Immunity: A Classroom Experiment," Alan Grant, Jim Bruehler, Andreea Chiritescu, Journal of Economics Teaching, 2016, vol. 1, issue 1, pages 7-16)
Policies with Varying Costs and Benefits: A Land Conservation Classroom Game (S. Dissanayake & S. Jacobson)
oTree
(  )
)
Ce jeu place les étudiants dans le role d'agriculteurs qui doivent choisir de cultiver ou pas leurs terres en fonction de différentes politiques de conservation des terres agricoles...
Il permet d'introduire, entre autres, les notions d'externalités et de biens publics. Le jeu convient pour des cours d'économie de l'environnement, d'économie agricole, ou de microéconomie.
("Policies with Varying Costs and Benefits: A Land Conservation Classroom Game ," by Sahan T. M. Dissanayake and Sarah A. Jacobson, The Journal of Economic Education 2016 47 (2), 142-160)
Vous pouvez décider de tirer au sort la position des joueurs à chaque tour ou les laisser sur le même emplacement pendant tout le jeu. Si vous sélectionnez plusieurs grilles, votre jeu comportera plusieurs "sous-jeux" identiques sur des grilles comparables. Par exemple, si vous choisissez 3 grilles de 4 lignes et 5 colonnes, le jeu impliquera 3*20=60 joueurs répartis sur 3 grilles identiques.
Les Logins and mots de passe apparaîtront dans une fenêtre (Attention: vous ne pouvez vous connecter qu'à un seul compte par navigateur).
The Carbon Trading Game (R. Fouquet)
oTree
(  )
)
"A simple game of the market for carbon dioxide tradable permits... As a pedagogical tool, this game benefits from simplicity ... and enables students to grasp the concepts and remember them through the intensity and fun of a trading 'pit'...
The experiences also provide substantial insights into the evolution of the carbon dioxide permit market, particularly related to the evolution of trade volume, permit prices and country strategies."
("The Carbon Trading Game," by Roger Fouquet, Climate Policy 2003 (special Emissions Trading issue), v.3, pp.143-55)
Les Logins and mots de passe apparaîtront dans une fenêtre (Attention: vous ne pouvez vous connecter qu'à un seul compte par navigateur).
The Red/Green Simulation (J. Bruehler, A. Grant & L. Ghent)
oTree
(  )
)
"Collective action problems are at the heart of many economic issues. Often, students have trouble comprehending how society ends up with a less than optimal outcome, and may incorrectly assume that someone must want the outcome that occurs. Correcting this error is made difficult by the biases that students bring to these issues...
The Red/Green simulation demonstrates the tension between self-interest and the social good in a context-free manner allowing students to see that these sub-optimal outcomes may not be desired by anyone, but instead can result from unhealthy systems of incentives."
("Teaching Collective Action Problems without Contextual Bias: The Red/Green Simulation," by James R. Bruehler, Alan P. Grant, and Linda S. Ghent, Journal of Economics and Finance Education, 2017, Vol. 16 , issue 1)
Les Logins and mots de passe apparaîtront dans une fenêtre (Attention: vous ne pouvez vous connecter qu'à un seul compte par navigateur).
Dilemme du prisonnier
Top 10!
(  )
)
Un dilemme du prisonnier répété.
| Joueur 1 / Joueur 2 | Compete | Cooperate |
|---|---|---|
| Compete | 1 , 1 | 5 , -1 |
| Cooperate | -1 , 5 | 3 , 3 |
Un jeu de poule-mouillée à n joueurs
(  )
)
Pour qu'un projet soit un succès, il faut qu'au moins un des membres d'une équipe se charge d'une tâche particulièrement désagréable. Les membres de l'équipe (les joueurs) doivent choisir simultanément de se charger de la tâche ou pas. Si les joueurs se comportent conformément à l'équilibre de Nash symétrique en stratégies mixtes, plus l'équipe compte de membres, moins souvent le projet réussit. Jeu répété.
Jeu de Matching Pennies asymétrique
(  )
)
Un jeu à somme nulle faussement symétrique (et absolument pas équitable). Une bonne introduction aux équilibres de Nash en stratégies mixtes.
| Joueur 1 / Joueur 2 | Heads | Tails |
|---|---|---|
| Heads | 5 , -5 | -1 , 1 |
| Tails | -9 , 9 | 5 , -5 |
Jeu de la guerre des sexes
(  )
)
Un jeu classique de guerre des sexes, tel que décrit ici. Jeu répété.
| Joueur 1 / Joueur 2 | Prefered Option | Second Option |
|---|---|---|
| Prefered Option | 0 , 0 | 4 , 2 |
| Second Option | 2 , 4 | 0 , 0 |
Jeu d'entrée simultanée (répété)
(  )
)
Un jeu d'entrée simultanée (répété). Une autre introduction aux équilibres de Nash en stratégies mixtes.
| Joueur 1 / Joueur 2 | Stay Out | Enter |
|---|---|---|
| Stay Out | 0 , 0 | 0 , 100 |
| Enter | 100 , 0 | -50 , -50 |
Beauty Contest
oTree
(  )
)
Chaque joueur doit choisir un nombre entre 0 et 100. Le vainqueur est le joueur dont le choix est le plus proche des 2/3 de la moyenne de tous les choix...
Le vainqueur reçoit 100 points et tous les autres ne reçoivent reçoivent rien. Si plusieurs joueurs gagnent, ils se partagent les 100 points.
Ultimatum Game
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme (en fonction de votre choix à la création du jeu, ils changeront de partenaire à chaque round ou pas). Dans chaque paire, les joueurs se voient assigner un rôle au hasard: "proposer" ou "responder", qu'ils gardent jusqu'à la fin du jeu.
Les deux joueurs d'une paire peuvent se partager 100 points. Le "proposer" fait une offre de partage à prendre ou à laisser au "responder", qui peut accepter ou refuser. Si le "responder" refuse, chaque joueur reçoit 0 point.
Matching Pennies
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme, et jouent 10 rounds de "Matching Pennies"...
Le joueur A choisit "Heads" or "Tails". Le joueur B doit deviner ce que le joueur A a choisi.
S'il a deviné juste, le joueur B reçoit 100 points et le joueur A ne reçoit rien. Sinon, il ne reçoit rien et le joueur A reçoit 100 points.
| Joueur A / Joueur B | Heads | Tails |
|---|---|---|
| Heads | 0 , 100 | 100 , 0 |
| Tails | 100 , 0 | 0 , 100 |
Traveler's Dilemma (K. Basu)
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme. Les joueurs sont des voyageurs qui reviennent d'une île lointaine dont ils rapportent le même objet d'art...
Les joueurs doivent simultanément et indépendamment déclarer la valeur de l'objet (entre 2 et 100 points):
Si les deux annoncent la même valeur, il recoivent tous les deux ce montant. S'ils annoncent des valeurs différentes, ils reçoivent le montant le plus faible. En plus, le joueur qui a demandé le moins reçoit un bonus de 2€, celui qui demande le montant le plus important subit une pénalité de 2€.
(Kaushik Basu, "The Traveler's Dilemma: Paradoxes of Rationality in Game Theory"; American Economic Review 1994.)
Trust Game
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme (en fonction de votre choix à la création du jeu, ils changeront de partenaire à chaque round ou pas). Dans chaque paire, les joueurs se voient assigner un rôle au hasard: Joueur A ou joueur B, qu'ils gardent jusqu'à la fin du jeu.
Au début de chaque round, le joueur A reçoit 100 points, le joueur B ne reçoit rien. Le joueur A peut donner une partie de ses 100 points au joueur B. Les points donnés par A sont triplés avant que B ne les reçoivent. Une fois que B a reçu les points, triplés, il peut, s'il le souhaite, renvoyer une partie de ses points au joueur A.
The Bargaining Game
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme. Les deux joueurs d'une paire peuvent se partager 100 points. Ils doivent simultanément et indépendamment réclamer une partie des 100 points.
Si la somme des demandes est inférieure à 100 points, chaque joueur reçoit ce qu'il a demandé. Sinon, les deux joueurs ne reçoivent rien.
The Stag Hunt
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme. Les joueurs de chaque paire vont chasser ensemble. Chacun doit choisir entre chasser un cerf (Stag) ou un lièvre (Hare). Chaque joueur a besoin de la collaboration de l'autre joueur pour réussir à chasser un cerf. Il peut attraper un lièvre seul, mais un lièvre vaut moins qu'un cerf.
| Joueur A / Joueur B | Stag | Hare |
|---|---|---|
| Stag | 200 , 200 | 0 , 100 |
| Hare | 100 , 0 | 100 , 100 |
Jeu Simultané Personnalisable (2 à 4 actions par joueur)
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme et jouent jusqu'à 10 rounds d'un jeu simultané.
L'enseignant choisit les gains à la création du jeu, ainsi que le nombre d'actions possibles pour chaque joueur.
| Joueur 1 / Joueur 2 | A | B |
|---|---|---|
| A | x , x' | y , y' |
| B | z , z' | t , t' |
Vous pouvez choisir les noms des stratégies (10 caractères alphanumériques ou moins) ou laisser les noms par défaut (A, B, C ou D). Les gains doivent être des entiers compris entre -10000 et 10000.
Le nombre de joueurs doit être pair. Les Logins and mots de passe apparaîtront dans une fenêtre (Attention: vous ne pouvez vous connecter qu'à un seul compte par navigateur).
Jeu Séquentiel Personnalisable (2x2)
oTree
(  )
)
Les joueurs sont regroupés aléatoirement par paire de façon anonyme et jouent jusqu'à 10 rounds d'un jeu séquentiel. L'enseignant choisit les gains à la création du jeu.
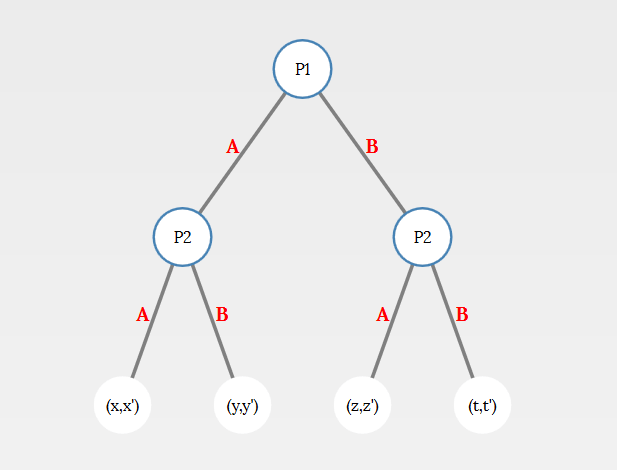
Les gains doivent être des entiers compris entre -10000 et 10000.
Le nombre de joueurs doit être pair. Les Logins and mots de passe apparaîtront dans une fenêtre (Attention: vous ne pouvez vous connecter qu'à un seul compte par navigateur).
Common Value Auction
oTree
(  )
)
Les joueurs doivent soumettre une offre pour un bien mis au enchère. Avant l'enchère, chaque joueur reçoit une estimation de la valeur du bien. Les estimations sont potentiellement différentes d'un joueur à l'autre, mais la valeur réelle du bien est la même pour tous, et n'est révélée qu'après la fin de l'enchère...
Chaque joueur présente une seule offre. Les offres se font sous pli fermé et sont dévoilées simultanément.
Le payoff du vainqueur, le joueur qui a soumis l'offre la plus élevée, est égal à la différence entre la valeur réelle du bien et la valeur de son offre. Si l'offre du vainqueur est supérieure à la valeur réelle du bien, son payoff sera négatif. En cas d'égalité entre plusieurs joueurs, le gagnant est tiré au sort. Les autres joueurs reçoivent un payoff équivalent à 0.
Vickrey Auction
oTree
(  )
)
Les joueurs sont regroupés aléatoirement avec deux autres participants de façon anonyme pour une enchère. Chacun d'entre eux reçoit 100 points au début du jeu...
Avant de soumettre une offre ils apprennent la valeur du bien qui est propre à chacun d'eux. La valeur du bien varie de manière aléatoire pour chaque participant entre 0 et 100.
Durant les enchères, ils soumettent anonymement une offre pour le bien (entre 0 et 100). Le joueur avec l'offre la plus élevée remporte le bien et paye la valeur de la seconde offre la plus élevée.
Le payoff du gagnant est calculé de la façon suivante (en point):
Payoff du gagnant = 100 + Valeur du bien pour le gagnant - Valeur de la seconde offre la plus élevée
Le payoff des autres joueurs restent de 100 points.
The Market for Lemons Game
oTree
(  )
)
Dans ce jeu, les joueurs sont regroupés aléatoirement avec deux autres participants de façon anonyme (en fonction de votre choix à la création du jeu, les groupes changeront à chaque round ou pas). L'un d'entre eux est un consommateur. Les deux autres joueurs sont des vendeurs. Les rôles sont définis de manière aléatoire et resteront inchangés jusqu'à la fin du jeu...
Au début de chaque tour chaque joueur reçoit 50 points. Les vendeurs commencent par déterminer un prix (entre 0 et 50) et un niveau de qualité pour leur bien. Ensuite le consommateur pourra choisir d'acheter l'un des deux biens à vendre, s'il le souhaite. Il n'observe que les prix et ne connait pas la qualité des biens, ni le vendeur qui est associé à chacun des biens. Après l'achat, les prix et le niveau de qualité sont dévoilés à l'ensemble des participants. Le niveau de qualité du bien peut être élevé, moyen, ou faible; Le niveau de qualité élevé a un coût production plus important et donne également un payoff plus élevé au consommateur. Le tableau suivant montre les coûts de production et la valeur que leur donne les consommateurs en fonction des différents niveaux de qualité (en point).
| Qualité | Haute | Moyenne | Basse |
|---|---|---|---|
| Coût de production des vendeurs | 30 | 20 | 10 |
| Valeur pour l'acheteur | 45 | 30 | 15 |
Durant un tour le consommateur peut acheter un seul bien et les vendeurs peuvent produire un seul bien. Les biens non vendus ne sont pas produits et ont donc un coût de 0.
Le payoff d'un tour pour le consommateur est de: Payoff du consommateur (pour un tour) = 50 + valeur associée à la qualité du bien acheté - prix du vendeur
Le payoff d'un tour pour le vendeur est de: Payoff du vendeur (pour un tour) = 50 + prix du vendeur - coût de production du bien (dépendant de sa qualité)
"Design a Contract: A Simple Principal-Agent Problem as a Classroom Experiment" (S. Gächter & M. Königstein)
oTree
(  )
)
Les joueurs possèdent une entreprise mais n'ont pas les compétences pour la diriger. Ils s'adressent donc à un expert et doivent définir le contrat à lui proposer: Un contrat consiste en un montant fixe, auquel s'ajoute un pourcentage des profits de l'entreprise. L'expert décide alors d'accepter ou non le contrat, et, s'il l'accepte, choisit le niveau d'effort (couteux) qu'il exerce (et qui impacte fortement les profits de l'entreprise)...
("Design a Contract: A Simple Principal-Agent Problem as a Classroom Experiment", Simon Gächter and Manfred Königstein, Journal of Economic Education 2009, 40, 173–187)
Contracting under Incomplete Information and Social Preferences (E. Hoppe and P. Schmitz)
oTree
(  )
)
"We consider a principal who can make a wage offer to an agent for the production of a good. The agent's production costs can be either low or high with equal probability. When the agent accepts the offer, he has to incur the production costs and the principal obtains a return. We consider a setting where the principal's return is larger than the production costs in both states of nature. Hence, ex post efficiency is achieved if the agent accepts the wage offer regardless of the state of nature...
To explore how contracting responds to changes in uncertainty, we have ...four main treatments, using a 2 x 2 design. In particular, we consider two different parameter constellations regarding the agent's production costs and two different information structures. One information structure is relatively simple (the agent always has private information about his production costs from the outset), while the other information structure is more complex (before signing the contract, the agent endogenously decides whether to spend resources to privately learn his production costs)."
(" Contracting under Incomplete Information and Social Preferences: An Experimental Study ," Eva I. Hoppe and Patrick W. Schmitz, Review of Economics Studies, 2013, vol. 80 (4), pages 1516-1544)
4 traitements différents sont possibles: sans acquisition d'information et avec plus ou moins de dispersion sur les coûts (AI 20-80 ou AI 40-60) / avec acquisition d'information et plus ou moins de dispersion sur les coûts (IG 20-80 aou IG 40-60). Vous pouvez choisir la variante à la création du jeu. Vous pourrez aussi la modifier à chaque round dans l'interface d'administration, à l'intérieur du jeu.
The Bubble Game (S. Moinas & S. Pouget)
Top 10!
oTree
(  )
)
Ce jeu sur les bulles spéculatives permet de discuter de l'efficience des marchés et des stratégies d'investissement dans un cours d'économie financière.
Les joueurs se revendent séquentiellement un actif, dont la valeur fondamentale est nulle. Si le prix des actifs n'est pas borné, des bulles spéculatives peuvent exister dans un équilibre de Nash, car aucun trader n'est jamais sûr d'être "le dernier à pouvoir acheter l'actif". Dans le cas contraire, l'équilibre de nash implique qu'il n'y a pas d'échanges. En pratique, des bulles sont généralement observées, dans les deux situations.
("The bubble game: A classroom experiment," Sophie Moinas and Sébastien Pouget, Southern Economic Journal, 2016, vol. 82(4), pages 1402-1412). Il existe une extension théorique et expérimentale de ce papier: "Learning in Speculative Bubbles: An Experiment" par Hong, Moinas et Pouget.
Notez qu'une simulation monojoueur (contre robots) existe, dans la rubrique "1 joueur".
Asymmetric Information Trading Game (B. Biais, D. Hilton, K. Mazurier & S. Pouget)
oTree
(  )
)
"... directly inspired by Plott and Sunder (1988). The value of an asset can be high (490), medium (240), or low (50). The traders observe different private signals. For example when the value of the asset is high, half the participants are privately informed that it is not low, while the others learn privately that it not medium.
Traders can place limit and market orders in a call auction and an open outcry continuous market. There is a strong winner’s curse risk in this trading game..."
("Judgemental Overconfidence, Self-Monitoring, and Trading Performance in an Experimental Financial Market," Bruno Biais, Denis Hilton, Karine Mazurier and Sébastien Pouget, 2005, Review of Economic Studies 72, 287–312.)
"A Classroom Investment Coordination Experiment" (D.Hazlett)
oTree
(  )
)
"Les joueurs sont des dirigeants d'entreprise qui doivent prendre une décision d'investissement (jeu répété).
Si un joueur anticipe un faible niveau d'investissement de la part des autres joueurs, il a intérêt à choisir lui aussi un faible niveau d'investissement, et contribue ainsi à provoquer une récession. Par contre, s'il anticipe une période d'expansion, il a intérêt à fortement investir, contribuant ainsi à la déclencher."
("A Classroom Investment Coordination Experiment", Denise Hazlett, IREE 2007, Volume 6, Issue 1, pp. 63-76, financé par la NSF)
A Classroom Inflation Uncertainty Experiment (D.Hazlett)
oTree
(  )
)
"This classroom experiment uses a double oral auction credit market to demonstrate how inflation uncertainty causes a wealth transfer between borrowers and lenders.
The experiment also shows the social cost of inflation uncertainty when borrowers and lenders cannot agree on a nominal interest rate that compensates each for their risk. In this case, the credit market fails to allocate funds to the highest-valued investment projects.
The experiment provides hands-on experience with the effects of anticipated and unanticipated inflation, giving students a common background for a discussion of the economic costs of inflation. It can be used in principles, intermediate macroeconomics,money and banking, or financial economics courses, with 8–60 students..."
("A Classroom Inflation Uncertainty Experiment", by Denise Hazlett, International Review of Economics Education 2008)
Pour toute question ou suggestion,